Геометрическая интерпретация

Векторы порождают p+1 –мерное подпространство π (рис.7.1).Рассмотрим векторы 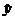и , определяемые следующими соотношениями

(7.27)

Очевидно, что вектор лежит в гиперплоскости (подпространстве) π.

Поставим задачу: найти такие , чтобы вектор e имел наименьшую длину. Другими словами мы хотим наилучшим образом аппроксимировать вектор y вектором , лежащим в гиперплоскости π. Очевидно, что решением является такой вектор , для которого вектор e ортогонален (перпендикулярен) плоскости π. Для этого необходимо и достаточно, чтобы вектор e был ортогонален векторам и , порождающим плоскость π (рис. 5.3). Т.е. вектор является ортогональной проекцией вектора на плоскость π. Вектор остатков ортогонален π.

Рис. 7.1 Геометрическая интерпретация построения уравнения регрессии

Т.е. фактически актуален рис.5.3 ЛР №5 [1] с заменой векторов, порождающих гиперплоскость π.