Свойства регрессионных остатков

⇐ Предыдущая 1 2 3 4 5 6 789 10 Следующая ⇒

Согласно второму условию Гаусса-Маркова для результативного применения МНК требуется, чтобы дисперсия остатков – разности значений исходных данных и данных, полученных по уравнению регрессии, была гомоскедастичной, т.е. однородной. Это значит, что для каждого значения фактора остатки 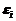имеют одинаковую дисперсию. При малом объеме выборки для оценки гетероскедастичности (нарушении гомоскедастичности) может использоваться метод Гольдфельда-Квандта (Goldfeld-Quandt). Основная идея теста Гольдфельда-Квандта состоит в следующем:

§ упорядочение n наблюдений по возрастанию X;

§ исключение из рассмотрения C центральных наблюдений; при этом 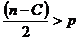, где 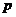– число оцениваемых параметров;

§ разделение совокупности из (n-C) наблюдений на две группы (соответственно с малыми и большими значениями Х) и определение по каждой группе уравнений регрессии;

§ определение остаточной суммы квадратов для первой (S₁) и второй (S₂) групп и их отношения F=S₁/S₂, если S₁>S₂ или F= S₂/ S₁, если S₁<S₂.

При выполнении нулевой гипотезы о гомоскедастичности отношение F будет удовлетворять F -критерию с числом степеней свободы для каждой остаточной суммы квадратов. Чем больше величина F превышает табличное значение , тем сильнее нарушена предпосылка о равенстве дисперсий остаточных величин. Если вычисленное значение больше 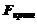, то следует учесть следующее:

§ средние квадратические ошибки коэффициентов регрессии будут занижены, что может привести к ложному выводу о значимости параметров уравнения регрессии;

§ полученные оценки параметров являются несмещенными оценками b_i, поэтому их можно использовать в уравнении;

§ на практике стандартные ошибки пересчитываются с помощью известных методов (White, Newey-West).

Согласно третьему условию Гаусса-Маркова для корректного использования уравнения регрессии требуется, отсутствие систематической связи (корреляции) между остатками. Для исследования поведения остатков, их упорядочивают по возрастанию фактора. Остатки индексируются величиной t. Наименьшему значению фактора соответствует t=1 и остаток e₁, следующему значению фактора соответствует t =2 и остаток e₂, и т.д. до значения t=n. Индекс t можно рассматривать как время и говорить о текущем и предшествующих моментах времени.

Автокорреляция в остатках – корреляционная зависимость между значениями остатков e_t за текущий и предыдущий моменты времени. Для определения автокорреляции остатков используют критерий Дарбина-Уотсона (Durbin-Watson). Для этого вычисляют величину по следующей формуле:

,. (7.29)

где -остаток предыдущего уровня.

Для значения выполняется соотношение . По таблицам находят два критических значения: нижний уровень - 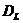и верхний - , значения которых зависит от количества наблюдений 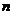, сложности модели (количества параметров) и выбранного уровня значимости. Если превышает 2, то это свидетельствует об отрицательной корреляции и перед сравнением его величину надо преобразовать: .

Если - модель неадекватна, остатки сильно автокоррелированы.

Если - остатки некоррелированы,модель адекватна.

Если 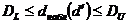- однозначного вывода сделать нельзя и необходимо применять другие критерии.

Если в остатках полная положительная автокорреляция, то , если полная отрицательная, то 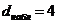, если автокорреляция остатков отсутствует, то .

Если обнаружена автокорреляция, то, как и в случае с гетероскедастичностью, следует помнить: стандартные ошибки будут занижены, что может привести к ложному выводу о значимости коэффициентов уравнения регрессии. При нарушении гомоскедастичности и наличии автокорреляции ошибок рекомендуется традиционный МНК заменять обобщенным методом (ОМНК), который применяется к преобразованным данным.

Весьма вероятна положительная автокорреляция остатков. Н₀ отклоняется. Зона неопределенности Нет оснований отклонять Н_0. Автокорреляция остатков отсутствует. Зона неопределенности Весьма вероятна отрицательная автокорреляция остатков.Н₀ отклоняется.

0 dL dU 2 4-dU 4-dL 4

Рис.7.3 Области принятия и непринятия гипотезы об автокорреляции остатков.

⇐ Предыдущая 1 2 3 4 5 6 789 10 Следующая ⇒

Не нашли, что искали? Воспользуйтесь поиском: