
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Множественная корреляция
Тесноту совместного влияния факторов на результат показывают коэффициент множественной детерминации и индекс множественной корреляции.
Качество построенной модели в целом оценивается коэффициентом множественной детерминации, который определяется формулой:
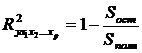 , (7.8)
, (7.8)
где  - остаточная сумма квадратов отклонений,
- остаточная сумма квадратов отклонений,
 - общая сумма квадратов отклонений значений
- общая сумма квадратов отклонений значений  от среднего арифметического значения отклика Y.
от среднего арифметического значения отклика Y.
Для линейной регрессии можно доказать следующее равенство:  , где
, где 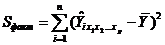 - факторная или регрессионная сумма квадратов отклонений.
- факторная или регрессионная сумма квадратов отклонений.
Остаточная сумма квадратов отклонений  характеризует суммарное отклонение наблюдаемых (эмпирических) данных от теоретических значений, найденных по уравнению регрессии. Факторная или регрессионная сумма квадратов отклонений
характеризует суммарное отклонение наблюдаемых (эмпирических) данных от теоретических значений, найденных по уравнению регрессии. Факторная или регрессионная сумма квадратов отклонений  характеризует разброс теоретических значений относительно среднего арифметического значения наблюдаемого значения (отклика).
характеризует разброс теоретических значений относительно среднего арифметического значения наблюдаемого значения (отклика).
Все свойства коэффициента детерминации  указаны в ЛР №5. Так, значение этого коэффициента лежит в пределах от 0 до 1. Это значение показывает долю объясненной вариации результативного признака (отклика) за счет включенных в уравнение p факторов, т.е. насколько хорошо уравнение, полученное с помощью регрессионного анализа, объясняет взаимосвязь между откликом и факторами. Доля необъясненной вариации отклика других, не учтенных в модели факторов, равна
указаны в ЛР №5. Так, значение этого коэффициента лежит в пределах от 0 до 1. Это значение показывает долю объясненной вариации результативного признака (отклика) за счет включенных в уравнение p факторов, т.е. насколько хорошо уравнение, полученное с помощью регрессионного анализа, объясняет взаимосвязь между откликом и факторами. Доля необъясненной вариации отклика других, не учтенных в модели факторов, равна  . Коэффициент детерминированности служит показателем тесноты связи между независимой переменной и факторами. Показателю тесноты связи можно дать качественную оценку (шкала Чеддока):
. Коэффициент детерминированности служит показателем тесноты связи между независимой переменной и факторами. Показателю тесноты связи можно дать качественную оценку (шкала Чеддока):
Таблица 7.1
Шкала Чеддок а
| Количественная мера тесноты связи | Качественная характеристика силы связи |
| 0,1-0,3 | Слабая |
| 0,3-0,5 | Умеренная |
| 0,5-0,7 | Заметная |
| 0,7-0,9 | Высокая |
| 0,9-0,99 | Весьма высокая |
Величину  для уравнения множественной регрессии в стандартизованном масштабе можно определить по формуле
для уравнения множественной регрессии в стандартизованном масштабе можно определить по формуле
 (7.9)
(7.9)
Индекс множественной корреляции  так же характеризует тесноту связи между факторами и откликом. Индекс множественной корреляции
так же характеризует тесноту связи между факторами и откликом. Индекс множественной корреляции  связан с коэффициентом множественной детерминации
связан с коэффициентом множественной детерминации  естественным соотношением.
естественным соотношением.
 (7.10)
(7.10)
Очевидно что, значение  лежит в пределах от 0 до 1. Также выполняется следующее соотношение
лежит в пределах от 0 до 1. Также выполняется следующее соотношение  , где
, где 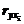 парный индекс корреляции.
парный индекс корреляции.
При линейной зависимости коэффициент множественной корреляции можно определить через матрицу парных коэффициентов корреляции:
 , (7.11)
, (7.11)
где 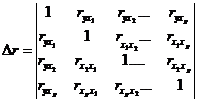 , (7.12)- определитель матрицы парных коэффициентов корреляции;
, (7.12)- определитель матрицы парных коэффициентов корреляции;
 -, (7.13)
-, (7.13)
определитель матрицы межфакторной корреляции, полученный из матрицы парных коэффициентов корреляции вычеркиванием первой строки и первого столбца.
Не нашли, что искали? Воспользуйтесь поиском: