Оценка надежности уравнения множественной регрессии

Проверить значимость уравнения регрессии - значит установить насколько хорошо математическая модель, выражающая зависимость отклика от факторов, согласуется с экспериментальными данными, с учетом количества наблюдений и количества факторов в уравнении.

Оценка значимости уравнения регрессии в целом сводится к проверке того, что величина не случайно отлична от нуля.

Для оценки значимости уравнения множественной регрессии в целом используется F -критерий Фишера.

Выдвигаем нулевую гипотезу : . Это возможно, когда уравнение регрессии незначимо, т.е. связь между откликом и факторами отсутствует. Альтернативная гипотеза : , в этом случае уравнение регрессии адекватно описывает связь между откликом и факторами.

Схема проведения дисперсионного анализа приведена в табл.7.2. Схемы применения F -критерия Фишера для оценки значимости уравнения множественной регрессии и уравнения парной регрессии одинаковы. Различие состоит только в одном – в определении числа степеней свободы 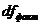и .

Существует соотношение между числом степеней свободы 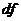(числом свободы независимого варьирования признака) для общей, факторной и остаточной сумм квадратов:

.

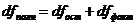Для множественной линейной регрессии:

,

где - число единиц совокупности, 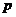- число факторов, включенных в уравнение регрессии.

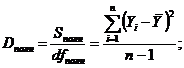(7.14)

(7.15)

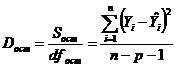. (7.16)

Таблица 7.2.

Не нашли, что искали? Воспользуйтесь поиском: