
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Теоретические сведения. Чаще всего в качестве факторов (объясняющих переменных) в регрессионных моделях рассматриваются экономические переменные
Чаще всего в качестве факторов (объясняющих переменных) в регрессионных моделях рассматриваются экономические переменные, принимающие количественные значения в некотором интервале. Вместе с тем может оказаться необходимым включить в модель фактор, имеющий два или более качественных уровней. Это могут быть разного рода атрибутивные признаки, такие, например, как профессия, пол, образование, климатические условия, принадлежность к определенному региону. Чтобы ввести такие переменные в регрессионную модель, им должны быть присвоены те или иные цифровые метки, т.е. качественные переменные должны быть преобразованы в количественные. Такого вида сконструированные переменные в эконометрике принято называть фиктивными переменными (“ dummy variables ”). Фиктивность состоит в том, что количественная переменная описывает качественный признак. В отечественной литературе можно встретить термины «структурные переменные» или «индикаторные переменные».
Фиктивными переменные, принимающие ровно два значения называются дихотомическими или бинарными.
Включение в модель фиктивных переменных может иметь цель отразить в модели неоднородность совокупности. По идее, можно построить уравнение регрессии для каждого элемента совокупности, а затем изучать различия между ними, но введение фиктивных переменных позволяет исследовать одно уравнение сразу для всех элементов совокупности. Однако нельзя рассматривать фиктивные переменные как панацею при применении методов регрессии к неоднородным данным.
Пример 1.
Рассмотрим применение фиктивных переменных для описания аварийности на перекрестке автомобильных дорог в зависимости от интенсивности движения и освещенности в различное время суток (возможные значения - дневное или ночное время). Предположим, что изучается линейная зависимость, которая в общем виде для совокупности обследуемых перекрестков имеет вид:

где y - количество аварий;
x – интенсивность движения(автомобилей/мин).
Аналогичные уравнения могут быть найдены отдельно для дневного времени:
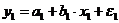
и ночного:
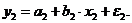
Различия в количестве аварий в зависимости от времени суток может проявиться в различии средних  и
и  . Вместе с тем сила влияния x на y может быть одинаковой, т.е.
. Вместе с тем сила влияния x на y может быть одинаковой, т.е. 
Положим
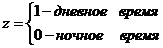
В этом случае возможно построение общего уравнения регрессии с включением в него фактора «время суток» в виде фиктивной переменной.
Например, включать в модель фактор «время суток» в виде фиктивной переменной можно в следующем виде:

Коэффициент регрессии при фиктивной переменной интерпретируется как среднее изменение зависимой переменной при переходе от одной категории к другой при неизменном значении остальных параметров. На основе t- критерия Стьюдента делается вывод о значимости влияния фиктивной переменной, существенности расхождения между категориями.
Предположим, что определено уравнение (т.е. методом наименьших квадратов вычислены коэффициенты A, С1 и b).
Теоретические значения размера аварийности в дневное время будут получены из уравнения

Для ночного времени соответствующие значения получим из уравнения

Сопоставляя эти результаты, видим, что различия в уровне аварийности для ночного и дневного времени состоят в различии свободных членов данных уравнений:  – для ночного и
– для ночного и 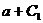 – для дневного.
– для дневного.
В этом примере существенным является, то, что угловые коэффициенты наклона прямых регрессии были приблизительно одинаковыми, т.е. выполнялось соотношение 
Однако в общем случае это не так, поэтому целесообразно учесть взаимодействие между факторами. Этот учет взаимодействия достигается путем введения в модель дополнительного слагаемого:

После того, как уравнение будет построено, следует последовательно проверить ряд гипотез:
1. Гипотеза  . Альтернативная гипотеза
. Альтернативная гипотеза  . Если гипотеза
. Если гипотеза  будет принята, то можно пользоваться одной моделью независимо от значения фиктивной переменной. Если будет принята гипотеза
будет принята, то можно пользоваться одной моделью независимо от значения фиктивной переменной. Если будет принята гипотеза  , то приходим к выводу, что модели не одинаковы.
, то приходим к выводу, что модели не одинаковы.
2. Если гипотеза  будет отвергнута, то можно проверить гипотезу
будет отвергнута, то можно проверить гипотезу  . Если
. Если  принимается, то заключаем, что уравнения регрессии имеют одинаковые углы наклона и отличаются только свободным членом.
принимается, то заключаем, что уравнения регрессии имеют одинаковые углы наклона и отличаются только свободным членом.
Если качественный признак принимает не два, а большее количество значений, то вводится не одна, а несколько фиктивных переменных по схеме, приведенной ниже.
Допустим, что требуется исследовать зависимость цены (Y) квартиры от ее площади (X) и типа дома (блочный, кирпичный, монолитный).
Фактор «тип дома» можно включить в модель в виде двух фиктивных переменных в следующем виде:


т.е. блочному дому соответствует комбинация (z1, z2)=(1, 0), кирпичному дому соответствует комбинация (z1, z2)=(0, 1), а монолитному дому соответствует комбинация (z1, z2)=(0, 0).
Пример 2.
Исследовать зависимость цены (Y) квартиры от ее площади (X) и типа дома (блочный, кирпичный). Таблица с данными приведена на рис.8.1.
Требуется:
1). Оценить визуально, построив соответствующие облака рассеяния величины Y в зависимости от Х, целесообразность использования линейного уравнения регрессии.
2). Построить модель (Модель - 0.), которая не содержит фиктивной переменной,
 ,
,
оценить ее качество. Проанализировать коэффициенты уравнения.
3). Построить две раздельные модели (Модель - 1 и Модель - 2), которые не содержат фиктивной переменной. При этом Модель - 1:  , только по данным, относящимся к блочным домам. Модель - 2:
, только по данным, относящимся к блочным домам. Модель - 2:  , только по данным, относящимся к кирпичным домам.
, только по данным, относящимся к кирпичным домам.

Рис.8.1.
Проанализировать коэффициенты уравнений и сравнить их между собой.
4). Построить Модель - 3, которая учитывает площадь и тип дома в едином уравнении множественной регрессии (ввести фиктивную переменную - Z - тип дома). Провести анализ этого уравнения, оценить значимость его параметров, пояснить их экономический смысл.
Решение.
К пункту 1.
Построим облако рассеяния данных(X-Y). (рис.8.2)

Рис.8.2.
Очевидно, что в этом облаке явно можно выделить две группы точек, одна из которых соответствует блочным домам, другая кирпичным.
К пункту 2.
Построим модель (Модель - 0.), которая не содержит фиктивной переменной.

Для определения коэффициентов воспользуемся графическими возможностями EXCEL и надстройкой «Пакет анализа»-«Регрессия». Результаты приведены на рис.8.3-8.4.

Рис.8.3.

Рис.8.4
Уравнение примет вид Y =1175.7 X -1456.5
Анализ полученных результатов показывает следующее:
Коэффициент детерминации R2 = 0.77 и он значим.
Свободный член (Y -пересечение) равен 1456.5 и он не значим.
Коэффициент b, равный 1175.7, значим. Этот коэффициент имеет простой экономический смысл - стоимость квадратного метра жилья без учета типа дома.
К пункту 3.
Построим еще две модели (Модель - 1 и Модель - 2.), которые не содержат фиктивной переменной.
При этом Модель - 1  будет построена только по данным, относящимся к блочным домам.
будет построена только по данным, относящимся к блочным домам.
При этом Модель - 2  будет построена только по данным, относящимся к кирпичным домам.
будет построена только по данным, относящимся к кирпичным домам.
Для определения коэффициентов воспользуемся графическими возможностями MS Excel и надстройкой «Пакет анализа» -«Регрессия».
Для Модели - 1 результаты приведены на рис.8.5-8.6.

Рис.8.5

Рис.8.6
Уравнение примет вид Y=997.7X+206.6.
Анализ полученных результатов показывает следующее:
R2 -= 0.99 и значим.
Свободный член (Y-пересечение) равный 206.6 не значим.
Коэффициент b равный 997.7, значим. Это значение имеет простой экономический смысл - стоимость квадратного метра жилья в домах блочного типа.
Для Модели - 2 результаты приведены на рис.8.7-8.8.

Рис.8.7
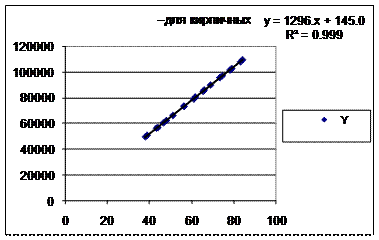
Рис.8.8
Уравнение примет вид Y=1296.4X+145.
Анализ полученных результатов показывает следующее:
R2 -= 0.99 и этот коэффициент значим. Свободный член (Y -пересечение) равен 145 и он не значим. Коэффициент b равен 1296.4, он значим. Это значение имеет простой экономический смысл – стоимость квадратного метра жилья в кирпичных домах.
Сравним три модели (Модель - 0, Модель - 1 и Модель - 2.) между собой (табл.8.2.).
Таблица 8.2.
| Модель - 1 | Модель - 2 | Модель - 0 | ||
| Y-пересечение | не значим | 206.6087862 | 145.0133857 | -1456.5196 |
| Стоимость, кв.м | значим | 997.7292019 | 1296.382158 | 1175.70579 |
| R-квадрат | значим | 0.999 | 0.999 | 0.78 |
Заметим, что стоимость квадратного метра различается в зависимости от типа дома (приблизительно 1000 и 1300 у.е. соответственно) и существенно различаются между собой.
Заметим, что для Модели - 0 R2=0,78 существенно ниже, чем для Модели - 1 и Модели - 2. Т.о. Модели - 1 и - 2 описывают ситуацию существенно лучше, чем единое уравнение в Модели - 0.
К пункту 4.
Попытаемся учесть влияние типа дома в едином уравнении.
Рассмотрим модель, которая содержат фиктивную переменную Z.
Модель - 3: Введем фиктивную переменную

Рассмотрим уравнение регрессии в виде

Поскольку стоимость квадратного метра существенно отличается, это учтено введением слагаемого 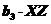 .
.
Для определения коэффициентов воспользуемся надстройкой «Пакет анализа» -«Регрессия». Для этого введем новую колонку для переменной (фактора) XZ (рис.8.9).

Рис.8.9
Результаты приведены на рис.8.10.
Получено уравнение:

Учет значимости коэффициентов проведен традиционным способом (рис.8.10).
 Рис.8.10
Рис.8.10
Вывод: С учетом значимости коэффициентов уравнение может быть записано в виде

Это уравнение имеет простой экономический смысл: стоимость квадратного метра в блочном доме 1000 (997,7) у.е., а в кирпичном стоимость квадратного метра на 300 (298.6) у.е. больше. Все коэффициенты в уравнении значимы.
Задание.
Исследовать величину заработной платы (Y, у.е.) работников некоторой компании в зависимости от суммы баллов, полученных на выпускных экзаменах в колледже (Х) и пола по плану, приведенному в примере 2.
Исходные данные взять из файла «Econometric_LabRab_8.xls».
Список ЛИТЕРАТУРЫ
1. Эконометрика.Парная регрессия. Методические указания к лабораторным работам / Санкт-Петербургский государственный горный институт (технический университет). Сост.: В.В. Беляев, Г.Н.Журов, Т.А. Виноградова, Т.Р. Косовцева. СПб, 2009., с.55
2. Магнус Я.Р. Эконометрика. Начальный курс. Учебник для вузов. - / Я.Р. Магнус, П.К. Катышев, А.А. Пересецкий; М., «Дело» 2000 г., 400 с.
3. Эконометрика./ Учебник для вузов. Под ред. Елисеевой И.И., М., «Финансы и статистика», 2004г., с.344.
4. Практикум по эконометрике./ Под редакцией Елисеевой И.И., М., «Финансы и статистика», 2004г., с.192.
5. Тихомиров Н. Эконометрика. Учебник / Н. Тихомиров, Е.М. Дорохина: М.: «Экзамен», 2006, с.512
6. Кремер Н. Ш. Эконометрика. Учебник для вузов, / Н.Ш. Кремер, Б.А. Путко М.: М.: Юнити, 2005, с.311
7. Арженовский С.В. Эконометрика: учебное пособие/ С.В. Арженовский, О.Н. Федосова Рост.гос.экон.университет – Ростов н/Д., 2002.- с102.
ОГЛАВЛЕНИЕ
Введение. 3
Лабораторная работа 7. Множественная регрессия 4
7.1. Теоретические сведения. Базовые понятия. 4
7.2. Множественная корреляция. 9
7.2. Оценка надежности уравнения множественной регрессии. 11
7.4. Скорректированный индекс множественной детерминации. 16
7.5. Частная корреляция. 17
7.6. Геометрическая интерпретация. 19
7.7. матричная форма записи. 20
7.8. Мультиколлинеарность факторов. 21
7.9. Свойства регрессионных остатков. 23
7.10.Отбор факторов при построении. 26
уравнения множественной регрессии. 26
Задание. 47
Лабораторная работа 8. Фиктивные переменные в множественной регрессии 48
Теоретические сведения. 48
Задание. 59
Список литературы.. 60
Не нашли, что искали? Воспользуйтесь поиском: