Мультиколлинеарность факторов

При построении уравнения множественной регрессии может возникнуть проблема мультиколлинеарности факторов.

Одним из условий построения корректной регрессионной модели является условие линейной независимости факторов. Если это условие нарушается, т.е. если один из факторов может быть выражен через несколько других, то говорят что, существует полная коллинеарность. Это порождает множество проблем. Например, применение формулы (7.18) невозможно, поскольку матрица 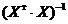не может быть вычислена (определитель ).

На практике полная коллинеарность встречается редко, гораздо чаще встречается ситуация, когда между факторами наблюдается высокая степень корреляции, и тогда говорят о наличии мультиколлинеарности факторов. В этом случае применение формулы (7.18) формально возможно, поскольку матрица 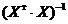может быть вычислена (определитель , но близок к нулю), поэтому полученные значения найденных коэффициентов будут обладать «плохими свойствами». Это можно объяснить, используя геометрическую интерпретацию МНК. Как показано выше, регрессия может быть рассмотрена как проекция в пространстве Rⁿ вектора y на подпространство, порожденное столбцами матрицы X (рис.7.1).

Если два фактора сильно коррелированны, то между векторами существует приблизительная линейная зависимость и угол между векторами (факторами) x₁ и x₂ мал(рис.7.2). В этом случае операция проектирования становиться неустойчивой, т.е. небольшое изменение в исходных данных может привести к существенному изменению оценок (значений) коэффициентов регрессии. Пусть векторы и 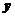это результаты двух различных серий наблюдений отклика при исследовании одной и той же проблемы. Эти результаты могут быть близки, но не обязательно совпадают. На рис.7.2 показано, что хотя векторы и мало отличаются друг от друга, но проекци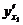и и 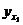разнонаправлены, т.е. отличаются друг от друга существенно. При разложении вектора по векторам x₁ и x₂ оба коэффициента будут положительны. При разложении вектора по векторам x₁ и x₂ коэффициент при x₁ принимает отрицательное значение. В силу этого интерпретация коэффициентов регрессии становится противоречивой, поскольку при использовании наблюдений, соответствующих вектору , приходим к выводу об увеличении отклика при увеличении фактора x₁, а при использовании наблюдений, соответствующих вектору к противоположному результату.

Рис.7.2 Геометрическая интерпретация построения уравнения регрессии при условии коллинеарности векторов (факторов) x₁ и x₂

Основные отрицательные проявления мультиколлинеарности заключаются в следующем:

· Значения найденных коэффициентов модели имеют неправильные с точки зрения теории знаки или неоправданно большие (маленькие) значения.

· Небольшие изменения исходных данных приводит к существенному изменению найденных коэффициентов модели

· Оценки имеют большие стандартные ошибки, малую значимость (хотя вся модель в целом является значимой).

· Невозможно оценить воздействие на отклик каждого фактора в отдельности.

Когда два фактора сильно коррелированы, говорят о коллинеарности факторов.

Считается, что два фактора явно коллинеарны, т.е. находятся между собой в линейной зависимости, если Из двух явно коллинеарных факторов уравнения регрессии рекомендуется один исключить. Предпочтение при этом отдается тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами.

Не нашли, что искали? Воспользуйтесь поиском: