Законы сохранения и свойства симметрии четырехмерного пространства.

Известно, что интегралы движения могут быть найдены из некоторых общефизических принципов (наряду с интуитивными способами). К примеру, в механике Ньютона закон сохранения импульса связан с однородностью пространства, а закон сохранения момента импульса – с его изотропностью.

Эти свойства имеют место и релятивистской механике, правда подразумевается, что из свойства однородности четырехмерного пространства следует закон сохранения четырехмерного импульса, а из свойства изотропности четырехмерного пространства следует закон сохранения четырехмерного тензора момента импульса .

Эти свойства можно вывести аналитически, заметив лишь, что наличие внешних полей, вообще говоря, приводит к нарушениям однородности и изотропности пространства. Однако, в некоторых направлениях или плоскостях эти свойства все же остаются неизменными. Поэтому, соответствующие проекции останутся интегралами движения.

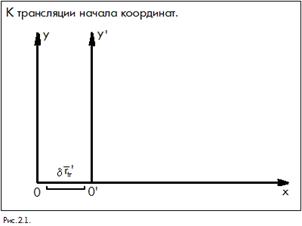
С математической точки зрения однородность пространства означает инвариантность уравнений движения относительно параллельного переноса системы координат. Под параллельным переносом подразумевается трансляция начала координат с одновременным сохранением ориентировки осей координат в пространстве.

Запишем преобразование трансляции. Для этого рассмотрим систему, начало координат которой транслируется вдоль оси на малый отрезок (здесь ) (рис. 2.1). в новой системе координат имеем преобразование , причем справедливо

.

для четырехмерного же пространства можно записать

.

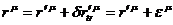В полученном выражении 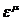представляет собой постоянный вектор, модуль которого равен переносу.

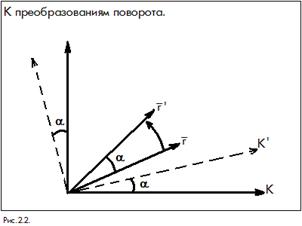Изотропность четырехмерного пространства в свою очередь означает, что уравнения движения являются инвариантными относительно поворота осей координат. Рассмотрим преобразования поворота осей координат, для простоты формально заменив поворот осей координат поворотом самого вектора и обозначив новое положение вектора за (рис. 2.2). Причем, угол поворота вектора тот же, что и угол поворота системы . Тогда для такого преобразования можно записать:

=> .

Перейдем теперь в четырехмерное пространство:

.

С другой стороны, преобразования поворота соответствуют преобразованиям Лоренца вида

.

Положим и перепишем эти преобразования как

.

И тогда

.

Тензор - тензор второго ранга. Если преобразования поворота являются бесконечно малыми, то коэффициенты являются малыми величинами.

Можно показать, что этот тензор является антисимметричным, то есть . Для этого найдем :

.

Для того, чтобы выполнялись условия инвариантности, необходимо, чтобы второй член в полученном выражении был бы равен нулю. Это возможно лишь в том случае, если тензор антисимметричен. Можно получить более конкретный вид для :

.

Отсюда, очевидно,

.

Рассмотрим теперь общее преобразование координат как сумму трансляций и поворотов осей координат:

.

и различаются на один порядок малости, и в выражении стоит , поэтому не существенно ставить штрих при или нет, потому как это будет ошибкой уже во втором порядке малости:

.

Таким образом, преобразования поворота выглядят как . Если использовать , то получаем выражение

.

Для того, чтобы уравнения движения были инвариантными относительно этих преобразований необходимо, чтобы вариация функции Лагранжа была бы равна нулю: 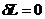. Функция Лагранжа есть функция координат и скорости: . Возьмем вариацию от функции Лагранжа:

.

Вариация от скорости находится как

.

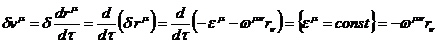Подставив вариацию скорости в выражение для вариации функции Лагранжа и опустив простые, но длинные преобразования, запишем конечное выражение:

.

Здесь на одном из этапов был использован тот момент, что для свободной частицы справедливо

,

чем и обусловлено появление импульсов в конечном выражении.

Так как коэффициенты преобразования координат являются произвольными и отличными от нуля, необходимым является равенство нулю самих производных. соответственно

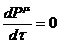и .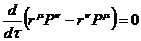

То есть, получен закон сохранения импульса для свободной частицы: . С другой стороны, по определению четырехмерный вектор импульса выглядит как

,

то есть в приведенном выше выражении скрыт также закон сохранения энергии свободной частицы.

Во втором выражении под знаком производной стоит конструкция

.

Этот тензор второго ранга называется тензором момента импульса. Это антисимметричный тензор, который выглядит следующим образом:

.

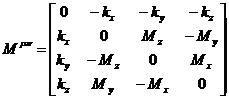Его производная, как было показано ранее, равна нулю, то есть 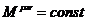. Для нахождения соответствующих компонент этого тензора следует воспользоваться следующей формулой, вывод которой приводиться не будет:

.

Для обратного преобразования существует формула

.

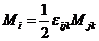Таким образом, все пространственные входят в трехмерный вектор момента импульса :

.

В свою очередь, временные компоненты образуют волновой вектор . Очевидно, что и вектор , и вектор - величины сохраняющиеся.

В конечном счете, задача состоит в том, чтобы найти десять интегралов движения (десять сохраняющихся величин). Они соответствуют десятипараметрической группе преобразований координат, которая представляет собой группу трансляций (4 преобразования) и группу пространственно-временных поворотов (6 преобразований). Эту группу называют группой Пуанкаре.

В этой группе постоянные 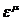и являются так называемыми структурными константами группы Пуанкаре, а сами интегралы движения и называются генераторами группы Пуанкаре.

Наличие внешнего поля приводит к нарушению свойств однородности и изотропности пространства. В соответствии с этим некоторые интегралы движения перестают быть таковыми (общее число интегралов движения уменьшается). Однако, может случиться, что в некоторых направлениях однородность и/или изотропность сохранятся, а значит и соответствующие компоненты и останутся интегралами движения.

Допустим, что используемая функция Лагранжа не зависит от одной из координат. Тогда соответствующая проекция обобщенного импульса будет сохраняющейся величиной. Действительно, предположим, что функция Лагранжа не зависит от . Тогда уравнение Лагранжа примет вид

.

Иначе это можно записать как

.

То есть - -проекция обобщенного импульса – сохраняющаяся величина. Если функция Лагранжа не зависит явно от времени, то сохраняться будет компонента . По определению

.

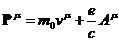Тогда для 0-компоненты:

,

,

.

Полная энергия, которая есть сумма кинетической и потенциальной, есть величина сохраняющаяся. То есть, получен закон сохранения для энергии .

То же происходит и с моментом импульса при наличии внешнего поля. Если в некоторой плоскости изотропность пространства сохраняется, то будем иметь в качестве интеграл движения соответствующий момент импульса. Например, если электрон движется в однородном поле, направленном вдоль оси Z, то , что несложно показать.

Не нашли, что искали? Воспользуйтесь поиском: