Вариационный принцип Гамильтона в релятивистской механике.

Соотношение определяет все уравнения движения. Это, собственно, и есть вариационный принцип Гамильтона, гласящий, что вариация действия для истинного движения должно равняться нулю. Следует ввести само понятие действия.

Согласно классической, нерелятивистской механике, действие выглядит как:

,

где 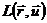- функция Лагранжа, описывающая состояние частицы. Таким образом, состояние системы в любой момент времени полностью определяется начальными значениями переменных и . В этом смысле функция Лагранжа является функцией состояния.

В релятивистской механике такое определение для действия уже не подходит, так как оно не удовлетворяет условию инвариантности вследствие неабсолютности времени. В таких условиях действие должно выглядеть как:

.

Следует оговориться, что функция Лагранжа является инвариантной. Способ построения инвариантной функции Лагранжа будет обсуждена много позже.

Перейдем непосредственно к взятию вариации от «нового» действия.

Для начала вкратце оговоримся, что здесь понимается под вариацией.

В нерелятивистской механике, если заданы истинные координаты 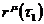и , заданные таким образом, что между ними возможны различные типы движения, то через них проходит бесконечное количество виртуальных траекторий, среди которых существует только одна истинная, по которой действительно происходит движение. Пусть вторая траектория истинная. Тогда вариацией будет множество всех отклонений значений от истинного в данный момент времени (изохронная вариация). Взятие вариации происходит по тем же правилам, что и взятие дифференциала, правда эти понятия различны. Выполняя дифференцирование, аргументу дается приращение и дифференциал есть разность функции для начального и конечного моментов интервала . То есть, это приращение, которое получает функция при изменении аргумента на величину . Дифференциал не изохронен, а вычисляется для бесконечно малого ненулевого отрезка времени.

Возьмем вариацию, пользуясь правилами взятия дифференциала:

.

Рассмотрим второй интеграл:

.

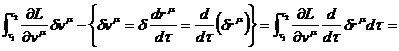
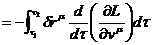В таком случае выражение для вариации действия выглядит как:

.

Так как 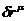является производной, то . Это означает, что нулю равняется выражение в квадратных скобках. Следовательно:

.

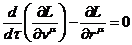Полученное выражение есть уравнение Эйлера-Лагранжа для релятивистской механики. Единственное отличие от нерелятивистского случая заключается в том, что здесь их не три, а четыре.

Заметим, что функция Лагранжа содержит произвол, который заключается в том, что она определяется с точностью до полной производной по времени от произвольной функции.

Не нашли, что искали? Воспользуйтесь поиском: