Четырехмерные тензоры.

Все физические величины есть тензоры различных рангов (нулевого, первого, второго и т. д.)

Тензором ранга нуль является такая величина, которая при переходе от одной инерционной системы в другую не претерпевает никаких преобразований (любые константы и инварианты есть тензоры нулевого ранга, например, скорость света).

Тензорами первого ранга являются четырехмерные вектора:

, где - тензор I ранга.

Примеры тензоров первого ранга - , , .

Тензором второго ранга называется совокупность 16 величин, которые при переходе от одной инерционной системы к другой преобразуются по закону:

.

Запишем тензор в общем виде:

.

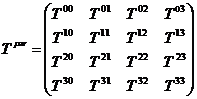Тензором ранга назовем совокупность чисел, преобразующихся по закону:

.

В дальнейшем будем называть тензором любой тензор II ранга, оговаривая особо случаи, когда используются тензоры более высоких рангов. Это обусловлено тем, что тензоры II ранга наиболее употребимы в курсе электродинамики. Итак будем рассматривать тензора II ранга.

Все тензоры делятся на симметричные и несимметричные:

- симметричный тензор

- антисимметричный тензор

Оказывается, что любой тензор можно представить как сумму симметричного и антисимметричного тензоров. Запишем произвольный тензор в виде:

.

Здесь, очевидно, первая скобка представляет собой симметричный тензор, а вторая – антисимметричный. Тогда это можно переписать как:

.

В дальнейшем мы будем иметь дело главным образом с антисимметричными тензорами. Нетрудно заметить, что у антисимметричного тензора все диагональные элементы есть нули, так как для любого из них справедливо , а следовательно, любой . Таким образом, произвольный антисимметричный тензор имеет вид:

.

Еще одним замечательным свойством тензоров такого рода является то, что если взять скалярное произведение (свертку) антисимметричного тензора с двумя одинаковыми векторами, то оно будет равно нулю: .

Покажем это:

.

Рассмотрим теперь преобразования Лоренца для конкретных компонент антисимметричного тензора. Рассмотрим для примеру компоненту , :

.

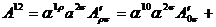
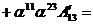
Говоря о последнем выражении, стоит вспомнить, что согласно вышеупомянутой метрике , при поднятии или опускании индексов знак не меняется, и лишь при поднятии или опускании «нулевого» индекса 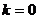знак меняется на противоположный.

Далее несложно найти преобразования для всех остальных компонент. Например, легко показать, что .

Тензоры, аналогично векторам, могут быть простраственноподобными и времяподобными. Соответственно, простраственноподобные тензоры есть такие тензоры, у которых компоненты с чисто пространственными индексами не равны нулю. Времяподобными тензорами являются тензоры, у которых не равны нулю компоненты, содержащие «нулевые» индексы.

Не нашли, что искали? Воспользуйтесь поиском: