Четырехмерное пространство и четырехмерная символика.

Так как время в СТО не является абсолютным, его можно рассматривать наравне с тремя координатами пространства как четвертую координату – координату времени. Такое пространство будем считать однородным и изотропным всюду, а все четыре оси – взаимно ортогональными. Как и оговаривалось ранее, будем называть такое пространство пространством Минковского. Координаты некоторой точки в таком пространстве образуют совокупность четырех величин:

, .

Определенная таким образом точка в четырехмерном пространстве точка называется мировой точкой. Если эта точка движется, то ее траектория называется мировой линией. Расстояние между двумя мировыми точками называется интервалом и определяется по формуле:

.

Под следует понимать расстояние, которое было определено ранее для простого трехмерного пространства.

Следует отметить, что интервал инвариантен. Иначе говоря, если есть интервал в одной инерциальной системе координат, а - в другой, то справедливо:

.

Из этого свойства интервала можно определить коэффициент в его определении. Запишем равенство интервалов:

.

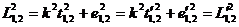Если время абсолютно, то при равенстве следовало бы, что , что и имело место в механике Ньютона.

Пусть теперь , а следовательно и . Инерциальные системы остаются таковыми, если они движутся относительно друг друга с постоянной скоростью. Рассмотрим две системы: и , движущуюся относительно с постоянной скоростью (рис. 1.8). В обеих системах координат скорость распространения света одинакова согласно первому постулату Эйнштейна - . Тогда можно записать:

.

Составим теперь квадрат интервала в четырехмерном пространстве:

=>

т.к. , то , => (знак «+» взят для определенности).

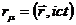Если теперь рассматривать радиус-вектор частицы в пространстве Миньковского, то его модуль можно записать как и следовательно . Таким образом .

В данном рассмотрении четвертая координата является мнимой, однако спустя некоторое время временнýю координату стали считать действительной. Для этого введем два типа четырехмерных векторов – контравариантные и ковариантные. Компоненты контравариантного вектора будут задаваться как , а ковариантного, соответственно, как . Тогда правило будет выполняться.

Позднее более широкую популярность приобрела другая система обозначений. Контравариантные вектора стали обозначать через , а ковариантные - . Для такой записи также легко убедиться, что:

– это тот же результат, что и с мнимой единицей. Однако в такой форме обозначений время является уже действительной координатой.

Далее для удобства будем считать, что все греческие символы пробегают значения от 0 до 3 - , а латинские – от 1 до 3 - .

В различных формулах электродинамики встречаются то верхние, то нижние индексы. Операция поднятия и опускания индексов производится посредством соответствующих метрических коэффициентов или метрики:

.

Конкретные коэффициенты принимают значения 0 или 1. Матрица имеет вид:

.

При этом будем считать, что при поднятии или опускании индекса 0 (1 раз!) знак меняется на противоположный, а когда мы поднимаем или опускаем индексы (1..3) ничего не меняется. Таким образом, получаем:

; .

Символ уже использовался при описании трехмерного пространства: – это -символ Кронекера.

Иногда в литературе используется другая метрика с сигнатурой –2, то есть сумма ее диагональных элементов равняется –2, а сама она имеет вид:

.

Впредь мы будем использовать исключительно метрику с сигнатурой +2: .

Не нашли, что искали? Воспользуйтесь поиском: