Четырехмерный вектор-потенциал и тензор напряженности электромагнитного поля.

Если в определении произвольного четырехмерного вектора за нулевую компоненту принять скалярный потенциал , а за векторную компоненту - трехмерный вектор-потенциал, то мы получим определение четырехмерного вектора-потенциала . С помощью этого вектора можно определить тензор напряженностей электромагнитного поля:

.

Из самого определения этого тензора следует, что он антисимметричен. антисимметричные тензоры и их основные свойства были достаточно подробно обсуждены выше. К примеру, мы можем беспрепятственно записать преобразования Лоренца для тензора напряженности, что, собственно, и будет проделано позднее.

Сейчас следует записать компоненты тензора 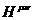. Так как тензор антисимметричен, то сразу можно сказать, что и . Таким образом, запишем:

.

Здесь - напряженность электрического поля, а - напряженность магнитного поля. Видно, что тензор состоит из шести взаимно независимых компонент и символически можно записать его как .

Оказывается, что все компоненты тензора 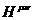можно вывести напрямую из его определения, и в результате получим:

Покажем это на примере компоненты , :

.

Фактически, эта запись означает, что:

- -компонента .

Из определения: . Тогда в общем случае это запишется как:

.

Аналогично можно показать, что формула для также напрямую следует из определения :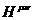

.

Откуда очевидно:

.

Тогда в общем случае справедливо записать:

.

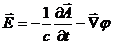Таким образом, было показано, что формулы для компонент тензора 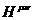, выведенные выше, справедливы и следуют напрямую из определения этого тензора.

Также вызывают интерес формулы, сопоставляющие четырехмерные и трехмерные векторы. На самом деле несложно показать, что между ними существует однозначное соответствие:

,

где - символ Леви-Чивита, принимающий значения 0, +1 и –1 в зависимости от значений индексов , и .

Для примера найдем -компоненту вектора напряженности магнитного поля :

.

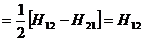Обратная формула имеет вид

.

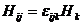Покажем теперь с ее помощью, что :

.

Иногда в электродинамике используется другой тензор электромагнитного поля, называемый дуальным к основному тензору или дуальным тензором. Дуальный тензор связан с основным следующим соотношением:

.

- тот же символ Леви-Чивита, но в четырехмерном пространстве.

Исходя из определения, дуальный тензор имеет вид:

.

Покажем, что дуальный тензор выглядит именно так. Проверим, например, что для дуального тензора :

.

Значит, согласно определению, дуальный тензор выглядит именно таким образом.

Теперь стоит перейти к нахождению преобразований Лоренца для компонент тензора 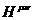. Собственно, эти преобразования находятся по аналогии с произвольным тензором простой заменой . К примеру, покажем, как выглядят преобразования Лоренца для -компоненты :

=> .

Для -компоненты:

=> .

Очевидно, что -компонента тензора 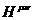не изменяется:

=> .

Таким образом, преобразования Лоренца выглядят как:

.

Аналогично можно записать преобразования Лоренца для компонент, содержащих нуль-индексы. В результате получим:

.

Также эти формулы можно получить в общем, векторном виде. Например, если перейти к нерелятивистскому приближению, то есть к случаю, когда и , и пренебречь 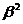, то можно записать эти формулы в трехмерном векторном виде.

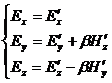и .

Тогда выражения для и выглядят:

Рассмотрим теперь следствия из преобразований Лоренца для напряженностей полей. Оказывается, это очень полезный инструмент для вычисления разного рода физических обстоятельств.

Так, с помощью преобразований Лоренца можно показать, что линии напряженности магнитного поля бесконечно длинного прямого проводника с постоянным током есть концентрические кольца. С одной стороны, это уже показано в курсе общей физики как формально, так и эмпирически, однако в данном случае можно подойти к этому выводу через преобразования Лоренца для магнитного поля (рис. 1.22).

Будем рассматривать ток как движение положительно заряженных частиц. Пусть заряд покоится в системе . Тогда очевидно:

=>

согласно формулам преобразования Лоренца. Следовательно, в лабораторной системе поля связаны как: .

Вектор направлен по радиус-вектору , а это значит, что направление вектора , являющегося векторным произведением на , будет всюду перпендикулярным к , а следовательно, и к радиус-вектору. Такому условию удовлетворяет только один тип кривых – окружности. Линии напряженности магнитного поля в рассмотренном примере есть окружности, лежащие в плоскости, перпендикулярной направлению протекания тока. Более того, стоит отметить, что густота линий напряженности тем больше, чем ближе они к проводнику.

В качестве другого примера применения преобразований Лоренца можно привести так называемый униполярный генератор тока. (Такое его название есть следствие того, что изначально полагали, что это генератор якобы с одним полюсом).

Рассмотрим принцип работы элементарного униполярного генератора на примере прямоугольного магнита, который может двигаться по ползунковым проводящим «рельсам» (рис. 1.23). Магнитное поле этого магнита пусть будет направлено вдоль оси . Во время движения магнита между рельсами возникнет поле , и, если подключить к ним, скажем, гальванометр или амперметр, они покажут наличие электрического тока. Чтобы вычислить это поле. Достаточно только учесть, что , а . Тогда , и поле находится как:

.

По сути, появление тока обусловлено напряженностью .

Примером униполярного генератора может служить массивный цилиндрический магнит, вращающийся вокруг своей оси с достаточно большой частотой. В такой системе напряженность направлена к оси вращения и возникает между осью и внешней поверхностью. Так что, если подключить через скользящие контакты к внешней стороне магнита и оси гальванометр, то он покажет наличие тока.

Для того чтобы обладать достаточной мощностью генераторы такого типа должны иметь большие размеры и вращаться с большими частотами. Так, например, униполярный генератор в Канберре, Австралия, имеющий ЭДС , состоит из магнита весом 20 тонн и компенсирующего маховика того же веса, вращающегося в обратную сторону. частота вращения магнита составляет порядка 900 оборотов в минуту.

§1.10. Инварианты электромагнитного поля.

Все тензоры имеют инварианты вида:

.

Это несложно показать. Действительно:

.

В составе электромагнитного поля существуют два тензора - 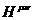и . На них можно построить три инварианта:

.

По сути, первый и третий инварианты означают одно и то же, поэтому рассмотрим два первых взаимно независимых инварианта.

Для начала вычислим первый из них, опуская дословное описание суммирования по каждому из индексов и :

.

То есть, для первого инварианта можно записать:

.

Аналогично можно вычислить и второй инвариант:

.

Второй инвариант выглядит как:

.

Рассмотрим теперь следствия из факта наличия этих двух инвариантов. В частности, первый из них гласит, что:

,

что означает, что если в одной системе отсчета и равны по модулю, то и в любой другой инерциальной системе отсчета они будут равны по модулю, что соответствует случаю, когда . Если же больше (меньше) нуля, то это означает, что если в одной системе отсчета больше (меньше) , то и в любой другой инерциальной системе отсчета будет больше (меньше) . Может случиться так, что в одной из систем , то в другой инерционной системе электрическое поле может быть и не равным нулю, но оно возникнет всегда таким образом, чтобы . И, соответственно, наоборот.

Если в одной системе угол векторы и ортогональны, то , а согласно второму инварианту и . А это значит, что и в любой другой инерциальной системе вектора останутся строго ортогональными. Более того, если в некоторой системе угол между ними острый (тупой) углом, то и в любой другой системе он будет острым (тупым). (Если в одной системе , то и в любой другой будет .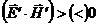

Не нашли, что искали? Воспользуйтесь поиском: