Преобразования Лоренца для скоростей и углов.

После того как были получены преобразования Лоренца для координат и времени, следует определить преобразования Лоренца для скоростей и углов.

Если взять дифференциал от преобразований Лоренца для координат и времени, полагая .

Исходя из определения для скорости , получаем для проекций скоростей:

Эти выражения есть преобразования Лоренца для скоростей. Убедимся теперь, что в нерелятивистском приближении мы получим вновь преобразования Галилея, пренебрегая выражением :

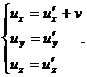
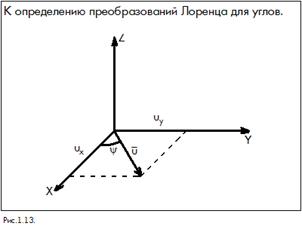
Убедимся также, что преобразования Лоренца для скоростей не приводят к парадоксу как в преобразованиях Галилея:

_.

Перейдем теперь к преобразованиям Лоренца для углов. Рассмотрим случай больших скоростей. Пусть в системе частица покоится (рис. 1.13). Тогда скорость в проекциях на оси и можно представить как:

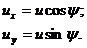
То же в системе:

Задача состоит в том, чтобы определить связь между и , для чего следует определит :

.

Будем считать теперь, что (это условие определения углов). Тогда

.

Чтобы избавиться от функции , запишем:

.

Откуда можно записать:

Аналогичным образом нетрудно показать, как выглядят преобразования Лоренца для телесного угла:

,

откуда можно напрямую записать, что

, где .

§1.5. Кинематические «парадоксы» СТО.

В этом параграфе будут рассмотрены четыре так называемых кинематических парадокса СТО.

Во-первых, рассмотрим «эффект прожектора». Пусть в «ракете», летящей со скоростью порядка скорости света человек светит («фонариком») в направлении перпендикулярном движению «ракеты» (рис. 1.14). Для наблюдателя со стороны :

.

Если , то ничего необычного наблюдаться не будет. Если же , то из предыдущего следует, что .

Этот эффект, в частности, наблюдается в современных ускорителях, где скорости электронов достигают скоростей порядка скорости света. В таких ускорителях при излучение электрона происходит практически по касательной к траектории, причем угол раствора для излучения электрона составляет секунды (рис. 1.15).

Во-вторых, имеет место эффект аберрации света, который впервые наблюдался Дж. Брадлеем в 1727-1729 гг. Во время годового обращения Земли вокруг Солнца, Брадлей заметил, что не стоят на месте, а движутся по небольшим эллиптическим орбитам. - направление движения Земли относительно стороннего наблюдателя в инерциальной системе отсчета. Наблюдатель на Земле увидит звезду -Дракона под углом (рис. 1.16).

Обратное преобразование Лоренца для :

.

.

Так как все эти преобразования проводятся для малых углов наблюдения, то справедливо:

.

Если теперь перевести радианы в секунды, то получим (рис. 1.17):

.

Здесь стоит отметить, что Брадлей в своих наблюдениях впервые положил скорость света , что было близко к современному значению скорости света.

В качестве третьего примера рассмотрим эффект замедления времени в движущейся системе координат. Пусть некоторая частица находится в начале координат системы и неподвижна относительно этой системы. (рис. 1.18) Тогда ее скорость относительно системы будет равна . Время, которое отсчитывается по часам в системе , где частица покоится, будем называть собственным временем и обозначать через 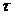. Время, которое отсчитывается наблюдателем в системе будем тогда называть лабораторным временем и обозначать через .

Если записать преобразования координат и времени, то получим:

будем считать, что , так как в системе частица покоится. Подставит выражение для в первую формулу:

,

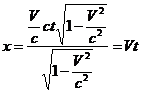что естественно для равномерно и прямолинейно движущейся в -системе частицы.

Из формулы преобразования времени тогда получаем:

.

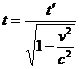Эта формула описывает замедление времени: . Физический смысл этого выражения заключается в том, что в движущейся системе координат время течет медленнее, чем в неподвижной системе наблюдателя (рис. 1.19). Отметим, что если частица движется с ускорением , то для малых отрезков времени это соотношение также будет выполняться и формула будет справедлива:

Если в начальный момент времени часы были синхронизированы, то уже через некоторое время движущиеся со скоростью часы будут запаздывать по отношению к неподвижным часам.

Имеется множество прямых и косвенных подтверждений эффекта замедления времени или, как более популярно, ­ эффекта близнецов. Наиболее убедительный способ – с использованием времени жизни космических частиц.

Космические лучи были открыты Гессом в 1912 г. Гесс рассматривал проблему ионизации в воздухе. Он наблюдал изменения в степени ионизации воздуха с высотой. С увеличением высоты ионизация увеличивалась.

Свинцовый ящик, в который был помещен электроскоп, поднимали на различную высоту. Подняв ящик на высоту 1400 метров и открыв его, Гесс он увидел, что листочки электроскопа опали. Чем больше высота, тем больше космических лучей разряжают электроскоп.

Эти лучи состоят в основном из протонов (~90%) и частично из 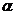-частиц. Время жизни -мезона . Время жизни -мезона . У поверхности земли или даже под землей обнаруживаются только -мезоны (рис. 1.20). -мезоны сильно взаимодействуют с атомами атмосферы. Длина пробега см. за счет того, что имеет место эффект замедления времени, время жизни у -мезонов увеличивается.

Ашер в 1972 г. проводил опыт с двумя самолетами, на борту которых были установлены сверхточные часы. В результате у самолета, летящего на восток, часы отставали от тех, которые были на земле.

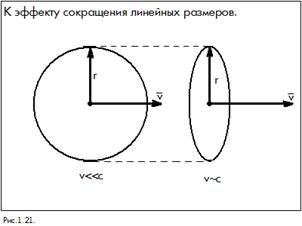Еще один немаловажный эффект – сокращение продольных размеров движущихся тел. Рассмотрим шар, который движется со скоростью порядка скорости света. Для стороннего наблюдателя этот шар будет выглядеть как диск (рис. 1.21). Рассмотрим опять две системы координат. В системе рассмотрим линейку длиной . В системе ее длина будет , причем:

.

Запишем преобразования Лоренца для приращений координат 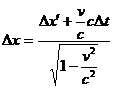и :

;

.

и должны быть измерены в один и тот же момент лабораторного времени.

;

=>

=> .

=> .

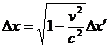Таким образом, линейные размеры движущегося тела для стороннего неподвижного наблюдателя уменьшаются в направлении движения при скоростях движения близких к скорости света.

Трехмерный объем, если его выбрать в виде куба с гранью параллельной оси , также будет подвержен продольному сжатию:

.

В данном случае роль сокращающегося отрезка будет играть .

Если теперь мы будем рассматривать четырехмерный элемент объема , то следует записать:

.

Это означает, что четырехмерный объем является инвариантом для преобразований Лоренца.

§1.6. Ковариантные формы преобразований Лоренца.

Ранее были получены преобразования Лоренца для координат и времени:

, где .

Эти формулы не являются ковариантными. Здесь выделены отдельные координаты и время, тогда как ковариантные формы подразумевают отсутствие выделенных координат.

, .

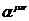- матрица, которая представляет собой коэффициенты преобразования. Эти коэффициенты постоянны.

.

Положим :

.

Сравнивая полученное выражение с известным преобразованием Лоренца, определяем соответствующие коэффициенты преобразования :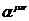

Положим теперь :

.

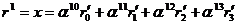Соответственно, находим:

Полагая далее и , получаем, что и . Все остальные коэффициенты равны нулю. Таким образом, матрица преобразования Лоренца для случая, когда система движется вдоль оси «неподвижной» системы имеет следующий вид:

.

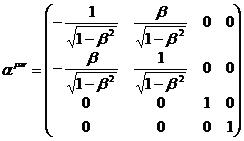Это – матрица частного преобразования Лоренца. Перепишем ее следующим образом:

.

Если речь идет об обратном преобразовании Лоренца, то вместо матрицы 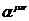следует использовать обратную матрицу :

.

Причем справедливо следующее выражение:

.

Очевидно, что , то есть :

.

Иначе, матрица удовлетворяет следующему условию:

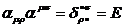- единичная матрица.

.

Следует убедиться в правдивости найденных коэффициентов. Для этого должно выполняться :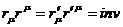

.

Несложно показать, что в случае произвольного преобразования Лоренца матрица преобразования выглядит таким образом:

.

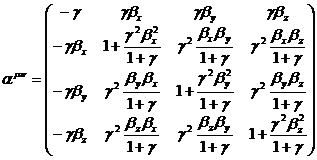Не нашли, что искали? Воспользуйтесь поиском: