Четырехмерные векторы.

Четырехмерные векторы – совокупность четырех величин, которые при переходе от одной инерционной системы отсчета к другой преобразуется по закону:

, .

Четырехмерный вектор скорости определяется как 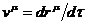, где 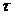- собственное время.

, где - обычная Ньютоновская скорость.

, так как .

Так же нетрудно показать, что :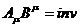

.

То есть свертка двух четырехмерных векторов есть инвариант. Найдем инвариант, соответствующий четырехмерному вектору скорости:

.

.

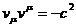Интересно, что в состоянии покоя (при ) будем иметь:

.

Такие четырехмерные векторы, у которых в системе компонент имеется только временная, называется временеподобными. Другим примером четырехмерных векторов служат пространствоподобные вектора. Таковым, например, является четырехмерный вектор ускорения:

- пространствоподобный вектор.

Найдем его компоненты:

.

Аналогично с радиус-вектором, введем производную по лабораторному времени:

.

Вычислим :

.

Подставим это значение в выражение для :

.

Фактически, это новый четырехмерный вектор. Перепишем это выражение, объединив 0-компоненты и пространственные компоненты:

.

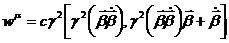Наконец, чтобы получить выражение, похожее на Ньютоновское ускорение . Для этого внесем в квадратные скобки и получим:

=>

=> .

Убедиться в его пространствоподобности можно, если рассмотреть в состоянии покоя :

=> .

Так образом, - пространствоподобный вектор. Можно показать, что четырехмерные вектора скорости и ускорения взаимно ортогональны в четырехмерном пространстве: . Покажем это:

=> =>

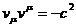=> => они взаимно ортогональны.

Также можно показать, что справедливо или иначе .

Стоит отметить, что введя понятие четырехмерного вектора, мы определяем преобразования Лоренца для четырехмерного вектора:

.

Запишем преобразования Лоренца для произвольного четырехмерного вектора:

.

Также можно доказать, что .

Не нашли, что искали? Воспользуйтесь поиском: