Преобразование Лоренца для координат и времени.

Необходимо определить такие преобразования инерциальных систем координат, чтобы 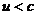. Этому условию удовлетворяют преобразования, для которых

.

Мы будем считать, что одна из точек, входящих в это преобразование, находится в начале координат. Покажем, что преобразования Галилея в таком случае не подходят:

.

Будем считать эти преобразования промежуточными (~), и позже они будут заменены на преобразования Лоренца. Подставим это преобразование в выражение для инварианта интервала:

.

Таким образом, видно, что инвариантность интервала при таком преобразовании не сохраняется, что противоречит утверждению об инвариантности интервала. Преобразуем теперь правую часть этого выражения к виду :

.

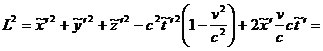
В последнем выражении была произведена замена:

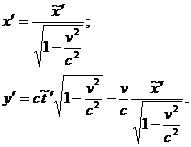
Если теперь выразить и подставить в преобразование Галилея, получим в итоге преобразования

Согласно преобразованиям Галилея :

.

Это и есть преобразование Лоренца для времени. Получим теперь преобразование Лоренца для координаты:

Окончательно, .

В итоге преобразование Лоренца для координат и времени выглядят следующим образом:

Для обратного преобразования, то есть перехода от к , следует только изменить знак у на и штрихованные величины сменить на нештрихованные. Несложно показать, что обратное преобразование Лоренца оставляет интервал инвариантом.

В нерелятивистском приближении преобразования Лоренца переходят в преобразование Галилея.

Действительно, будем считать, что , а следовательно :

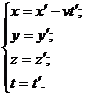
Видно, что преобразования Галилея являются предельным случаем преобразования Лоренца, когда 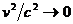. То есть принцип соответствия между двумя теориями соблюден.

Если в системе частица покоится, то ее скорость относительно системы равна скорости системы относительно этой системы. То есть преобразование Лоренца выполняется для частиц, движущихся с релятивистскими скоростями.

Также нетрудно показать, что в нерелятивистском приближении выражение:

.

Не нашли, что искали? Воспользуйтесь поиском: