Вывод силы Лоренца.

Главным объектом для изучения в электродинамике является заряд, находящийся во внешнем электромагнитном поле. Поэтому сила, действующая на заряд со стороны электромагнитного поля, является основной силой в электродинамике. Она называется силой Лоренца.

Сила Лоренца определяет уравнения движения заряда.

Для определения силы Лоренца необходимо задать конкретный вид функции Лагранжа для заряда, находящегося во внешнем поле. Известно, что функция Лагранжа есть функция координат и скорости: . Более того, известно, что . Руководствуясь соображениями простоты изложения, будем вести рассуждения для случая свободной частицы. Функция Лагранжа в таком случае может зависеть от ряда скалярных произведений - инвариант, как то (I), (II), (III). В первом случае функция Лагранжа зависит от того или иного места в пространстве, то есть нарушается принцип однородности пространства. Во втором случае входит скалярное произведение , что приводит к тому, что функция Лагранжа зависит от угла между и , что в свою очередь означает нарушение принципа изотропности пространства.

Будем рассматривать случай зависимости функции Лагранжа от инварианта для случая свободной частицы без внешних полей:

.

Запишем соответствующее уравнение Лагранжа:

.

Так как рассматривается случай свободной точки, когда функция Лагранжа не зависит от положения явно, очевидно имеем и окончательно уравнение Лагранжа запишется как

Запишем теперь функцию Лагранжа в явном виде в уравнение и возьмем производную по :

.

Отсюда видно, что в таком случае импульс и, следовательно, скорость свободной частицы является постоянной величиной.

Если же частицу (или заряд) поместить во внешнее поле, то вид функции Лагранжа усложнится. В нее войдут функция Лагранжа , описывающая движение свободной частицы, и , описывающая взаимодействие частицы (заряда) с полем:

.

Причем, также должна быть инвариантной. Таким образом, общая функция Лагранжа будет выглядеть как

,

где есть четырехмерный потенциал. Вообще, потенциал определяет взаимодействие заряда с внешним полем.

В этом случае частные производные функции Лагранжа будут иметь следующий вид:

.

Здесь - немой вспомогательный индекс, помогающий избежать путаницы между выходными индексами и индексами, по которым происходит суммирование. И, наконец, уравнение Лагранжа запишется как

.

Взяв соответствующие производные и вспомнив, что четырехмерный вектор ускорения есть , получим:

.

Наконец, воспользовавшись тем фактом, что , запишем

.

Выражение слева есть ни что иное как сила, а скобка в правой части есть определения тензора электромагнитного поля 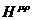. Таким образом, было получено выражение для силы, являющейся представлением силы Лоренца, которое имеет вид

.

Найдем теперь компоненты силы Лоренца.

.

Несложно показать, что, например, первая компонента силы Лоренца выглядит как

,

и, следовательно,

.

Таким образом, четырехмерный вектор силы Лоренца имеет вид

.

Иначе:

В слабом нерелятивистском приближении, то есть в случае, когда и , выражение для силы Лоренца принимает вид

.

Вторая часть выражения, умноженная на , представляет собой трехмерный вектор силы Лоренца в нерелятивистском случае.

Нулевая компонента выглядит как

.

Смысл нулевой компоненты заключается в том, что она соответствует закону сохранения энергии в случае стационарных полей. Это можно показать следующим образом: запишем через потенциал:

.

Тогда нулевая компонента запишется через

.

Если поле стационарно, то производная и, следовательно,

.

Запишем тогда нулевую компоненту силы Лоренца следующим образом:

=>

=> => .

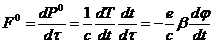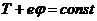Но известно:

, ,

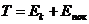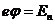Энергия покоя по определению. Но тогда справедливо

,

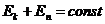что и требовалось показать.

Не нашли, что искали? Воспользуйтесь поиском: