Тензор спина и малая группа Лоренца.

Вообще, спин есть собственный угловой момент элементарной частицы. Так, к примеру, для электрона спин . Это квантовое явление, и его проекция – – имеет место лишь для определенно выбранных направлений.

По теории Уленбека и Гаудсмита электрон должен обладать собственным механическим угловым моментом и соответствующим ему собственным магнитным моментом, который равен магнетону Бора.

Рассмотрим метод, которым можно ввести понятие спина в квантовую теорию.

Известно, что угловой момент движущейся частицы определяется тензором

.

Этот тензор является антисимметричным и определяется как

.

В свою очередь трехмерный вектор момента импульса (пространственная часть соответствующего тензора) определяется через векторное произведение и в системе покоя обращается в нуль:

.

Пространственно-временная же часть тензора в системе покоя в нуль не обращается:

.

Иначе говоря, тензор временеподобный.

Будем определять спин с помощью тензора , причем этот тензор – пространственноподобный: . Для этого тензора будет справедливо выражение . Раскроем это суммирование, положив при этом :

.

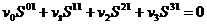Так как тензор антисимметричный, член равен нулю за счет равенства нулю элемента . С другой стороны, распишем тензор :

.

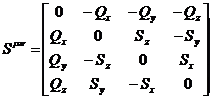Тем самым, имеем:

.

.

Иначе говоря,

.

В системе покоя этот вектор должен обращаться в нуль. Действительно,

.

Определим теперь некоторые свойства тензора :

ü Так как тензор антисимметричный, он будет иметь шесть независимых компонент.

ü Вследствие свойства пространственноподобности из этих шести компонент независимыми останутся только три.

ü Тензор спина, как и все другие тензоры, обладает инвариантом

.

В гипотезе Уленбека и Гаудсмита этот инвариант был определен как или, что то же,

.

Тем самым независимыми остаются лишь две компоненты – две степени свободы спина.

Отметим, что макроскопический угловой момент, определенный ранее, следует теперь называть орбитальным моментом , в отличие от спинового момента . В итоге, полный момент складывается из орбитального и спинового моментов:

.

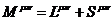Также несложно показать, что спиновый инвариант, именуемый инвариантом Любаньского-Паули, имеет следующий вид:

.

Рассмотрим, с каким свойством пространства связан закон сохранения спинового момента. Как уже упоминалось ранее, спиновый инвариант определен как

.

Чтобы учесть спиновый момент необходимо сделать замену вида

, .

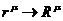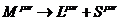Теперь, если повторить те же рассуждения, что были проведены ранее для закона сохранения момента импульса, то соответствующий закон сохранения будет получен из условия, что вариация функции Лагранжа должна быть равной нулю:

.

Если потребовать, чтобы 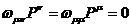, то первый член обернется в нуль.

Таким образом, мы получили, что преобразования пространственно-временного поворота в плоскости, перпендикулярной четырехмерному импульсу, являются преобразованиями симметрии при условии сохранения спинового момента. Такие повороты называют преобразованиями поворота из ­ малой группы Лоренца (группа Пуанкаре может называться полной группой Лоренца):

.

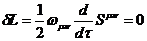Так как остается произвольным поворотом в перпендикулярной к скорости плоскости, , но тогда и

=> –

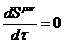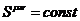спин обладает двумя степенями свободы.

Не нашли, что искали? Воспользуйтесь поиском: