
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Уравнение Баргмана-Мишеля-Телледи.
Уравнение Баргмана-Мишеля-Телледи – это уравнение движения спина во внешних электромагнитных полях. В некотором смысле, это аналог силы Лоренца.
Согласно гипотезе Уленбека-Гаудсмита, справедливы следующие утверждения:
ü Электрон имеет собственный механический момент за счет своего вращения, который равен
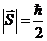 .
.
ü Электрон имеет собственный магнитный момент, равный магнетону Бора:
 .
.
ü Векторы магнитного и механического моментов электрона пропорциональны друг другу:
 .
.
Очевидно также, что они параллельны. Иначе последнее утверждение можно записать как
 .
.
Следует заметить, что в этих соотношениях все величины взяты для случая покоящегося электрона.
С точки зрения современной квантовой электродинамики, значение магнитного момента все-таки немного отличается от магнетона Бора и его можно записать в виде
 ,
,
где  - аномальный магнитный момент электрона, появляющийся за счет взаимодействия электрона с электрон-позитронным вакуумом. Если за
- аномальный магнитный момент электрона, появляющийся за счет взаимодействия электрона с электрон-позитронным вакуумом. Если за  обозначит фактор Ланде, который для электрона примерно равен двум, то это выражение можно записать как
обозначит фактор Ланде, который для электрона примерно равен двум, то это выражение можно записать как
 .
.
Аномальный магнитный момент впервые был подсчитан американским физиком Швингером в??49 году. Швингер определил значение фактора Ланде как
 ,
,
где  - первая поправка. Здесь
- первая поправка. Здесь 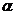 - постоянная тонкой структуры:
- постоянная тонкой структуры:
 .
.
Эта малая поправка играет большую роль в динамике электрона. В этом случае аномальный момент можно записать следующим образом:
 .
.
Если же учесть, что  , то
, то
 .
.
Согласно экспериментальным данным, фактор Ланде для электрона равен

(современные эксперименты дают колоссальную точность – до двенадцатого знака после запятой!).
Необходимо заметить, что в этих данных добавка к магнитному моменту, хоть и малая, но все же константа  .
.
Также, оказывается, что это утверждение справедливо лишь для слабых электромагнитных полей. Позже, в работе Бордовицына-Багрова-Чернова было показано, что магнитный момент электрона есть весьма сложная функция энергии электрона и величины магнитного поля.
Найдем теперь уравнение движения спина. Идея вывода состоит в том, что в начале определяется спина в системе покоя, а затем осуществляется ковариантный переход (или преобразования Лоренца) в лабораторную систему. Также делается предположение о том, что в системе покоя движение спина должно быть таким, чтобы оно не сопровождалось самопроизвольным выделением энергии.
Пусть  .
.
Прецессия есть движение, при котором одна компонента углового момента есть постоянная в течение всего времени величина, а две другие компоненты зависят от времени гармоническим образом, но в среднем равны нулю:

 ,
,  (рис. 2.3).
(рис. 2.3).
Прецессия единичного вектора описывается формулой Лармора:
 , где
, где  .
.
Выведем формулу Лармора. Возьмем сначала  (рис. 2.4). Тогда
(рис. 2.4). Тогда  и
и 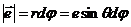 или
или  . Вектор связи между вращающимся вектором
. Вектор связи между вращающимся вектором  и углом поворота
и углом поворота  . Для получения формулы Лармора необходимо продифференцировать это выражение по времени:
. Для получения формулы Лармора необходимо продифференцировать это выражение по времени:
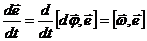 .
. 
Вернемся к описанию движения спина. Роль прецессирующего вектора в нашем случае играет вектор  , а роль времени – собственное время
, а роль времени – собственное время 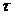 :
:
 – уравнение прецессии спина в системе покоя.
– уравнение прецессии спина в системе покоя.
Частота  уже известна – она совпадает с частотой обращения заряда в однородном электромагнитном поле:
уже известна – она совпадает с частотой обращения заряда в однородном электромагнитном поле:
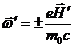 – циклотронная частота.
– циклотронная частота.
Так как мы рассматриваем спин электрона, нам нужен знак "минус" в определении циклотронной частоты. Также следует учесть, что электрон обладает аномальным магнитным моментом. Частота  с учетом фактора Ланде может быть записана следующим образом:
с учетом фактора Ланде может быть записана следующим образом:
 .
.
На самом деле, тот факт, что частота прецессии спина электрона совпадает с частотой обращения заряда в электромагнитном поле, является весьма примечательным. Это означает, что электрон в ходе вращения постоянно обращен одной и той же стороной, если, конечно, допустить, что возможно различить разные стороны электрона. В этом смысле его движение схоже по характеру с движение Луны вокруг Земли.
 Здесь стоит отметить, что в случае, если бы фактор Ланде равнялся бы в точности двум, после полного оборота, совершенного электроном в магнитном поле, его спин был бы направлен в точности так же, как и в начальный момент времени. Однако, за счет того, что фактор Ланде лишь весьма близок к двум, после полного оборота спин направлен несколько иначе, чем первоначально (рис. 2.5).
Здесь стоит отметить, что в случае, если бы фактор Ланде равнялся бы в точности двум, после полного оборота, совершенного электроном в магнитном поле, его спин был бы направлен в точности так же, как и в начальный момент времени. Однако, за счет того, что фактор Ланде лишь весьма близок к двум, после полного оборота спин направлен несколько иначе, чем первоначально (рис. 2.5).
В таком случае формула Лармора запишется как
 .
.
Разделим это выражение на  :
:
 .
.
Запишем то же выражение в ковариантном виде:
 .
.
Это – ковариантная форма записи прецессии спина в системе покоя.
Соответственно, в лабораторной системе
 .
.
Необходимо проверить, верна эта формула или нет. Известно, что
 .
.
=>  .
.
Действительно,
 .
.
С этой точки зрения полученная формула верна.
С другой стороны, известно, что  должен быть пространственноподобным. Несложно показать, что полученный таким образом вектор спина пространственноподобным не является, и спиновое уравнение нуждается в поправке, добавка которой удовлетворит свойствам четырехмерного вектора спина без потери ковариантности.
должен быть пространственноподобным. Несложно показать, что полученный таким образом вектор спина пространственноподобным не является, и спиновое уравнение нуждается в поправке, добавка которой удовлетворит свойствам четырехмерного вектора спина без потери ковариантности.
Баргман, Мишель и Телледи предложили поправку вида  , где для выполнения второго условия необходимо определить
, где для выполнения второго условия необходимо определить  так, чтобы второе условие выполнялось. Из условия равенства нулю производной от вышеупомянутого инварианта, для
так, чтобы второе условие выполнялось. Из условия равенства нулю производной от вышеупомянутого инварианта, для  было получено значение
было получено значение
 .
.
В итоге, полученное уравнение
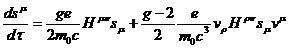
носит название уравнения Баргмана-Мишеля-Телледи.
Не нашли, что искали? Воспользуйтесь поиском: