II пара уравнений Максвелла при наличии зарядов и токов.

В случае присутствия в системе зарядов и токов функция действия будет состоять из трех слагаемых:

,

где - функция действия только для частиц (зарядов); - функция, учитывающая взаимодействия зарядов с полем; - функция действия для чистого поля.

, , .

Тогда:

.

Коэффициент носит эмпирический характер и возникает вследствие необходимости совпадения уравнения с экспериментом. Таким образом, условие 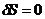примет вид:

.

Так как в данном случае нас интересуют уравнения для поля, будем считать, что движение зарядов уже задано, и можно считать, что

.

Таким образом, необходимо рассмотреть условие .

Однако, величина определена в терминах механики частиц. Следует задать ее в терминах теории поля, то есть совершить переход

.

В итоге действие будет одно и то же, но интеграл будет записан по-другому.

Для этого перейдем от заряда к его представлению через и внесем его под интеграл:

.

Нам известно, что четырехмерный вектор скорости имеет вид

,

где, следует заметить, не является четырехмерным вектором в полном смысле этого слова. Это есть лишь совокупность четырех величин. Тогда выражение

за счет того, что произведение является инвариантом. Но с другой стороны есть четырехмерный вектор плотности тока . Этот вектор имеет вид

.

Теперь можно записать

,

и, следовательно,

.

Путем дифференцирования по , получаем

.

Это и есть вторая пара уравнений Максвелла при наличии зарядов и токов. В развернутой форме это можно записать как

.

Если учесть, что - есть ток смещения, то второе уравнение можно переписать

,

где - полный ток.

Следствием второй пары уравнений Максвелла является уравнение непрерывности плотности тока.

Действительно, если считать ток постоянным, то можно записать

.

Если теперь продифференцировать по , то получим

,

,

.

Раскрыв суммирование по , получаем выражение

=> .

.

Учитывая то, что выражение есть полная производная по времени, получаем уравнение непрерывности плотности тока:

.

Не нашли, что искали? Воспользуйтесь поиском: