Вариационный принцип Гамильтона в теории поля.

Необходимость введения вариационного принципа в теорию поля очевидна на основании того факта, что необходимо получить уравнения движения. Для истинного движения вариация действия должна равняться нулю:

.

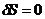Далее определяется действие, находится вариация от него и приравнивается к нулю.

В теории поля мы имеем дело с полевыми величинами, которые есть функции координат и времени.

В механике частиц все определялось радиус-векторами положений частиц в определенных точках пространства. В этом случае действие имело вид

.

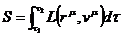Можно ввести действие в теории поля, однако будет иметь место ряд отличий:

ü Вместо радиус-вектора 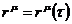необходимо ввести полевую величину, характеризующую электромагнитное поле. Такой величиной является потенциал .

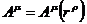ü Вместо скорости 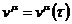необходимо ввести, по аналогии, величину .

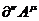ü Вместо функции Лагранжа 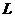, теряющей свой смысл в теории поля, необходимо ввести плотность функции Лагранжа 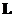, которая, что важно, остается инвариантной величиной.

ü Вместо интегрирования по собственному времени 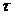необходимо ввести интегрирование по четырехмерному объему .

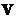Для того, чтобы сохранить размерность действия, домножим все на размерный инвариантный множитель :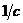

.

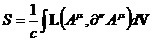Возьмем теперь вариацию от действия полученного вида:

.

Рассмотрим второй член подкоренного выражения:

,

.

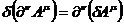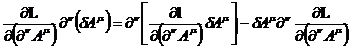Тогда интеграл запишется как

,

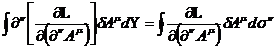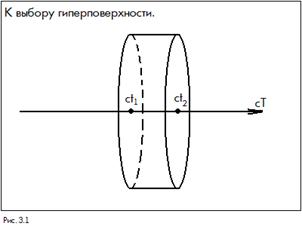где 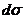- элемент гиперповерхности. Гиперповерхность можно выбрать произвольно; выберем ее в виде гиперцилиндра с образующей, параллельной оси 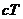. По сути этот гиперцилиндр образован двумя пространственноподобными плоскостями, соединенными временеподобной поверхностью. Интеграл по этой замкнутой гиперповерхности равен нулю.

Будем считать, что исследуемые функции на этих гиперплоскостях заданы и, более того,

.

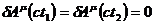Устремим теперь "радиус" гиперцилиндра к бесконечности. Если система замкнута, то вся она должна быть сосредоточена внутри ограниченного пространства. Следовательно, на бесконечности (в трехмерном смысле) полевые функции должны обращаться в нуль. Но это означает, что подынтегральное выражение есть нуль и, значит,

.

Таким образом, в выражении для вариации действия остается один член и окончательно имеем:

.

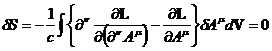Так как всюду , интеграл равен нулю только если нулю равно выражение в фигурных скобках. Тем самым получаем уравнение

,

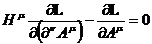которое является уравнением Эйлера-Лагранжа для поля.

Здесь стоит заметить, что плотность функции Лагранжа определена с точностью до четырехмерной дивергенции от произвольной функции координат и времени:

.

Несложно показать, что этот произвол не вносит никаких изменений в вариацию действия:

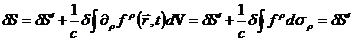, так как .

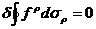Не нашли, что искали? Воспользуйтесь поиском: