I пара уравнений Максвелла в интегральной форме.

Уравнения Максвелла в интегральной форме очень удобны при рассмотрении геометрии и различных граничных условий для магнитного поля.

Рассмотрим первую пару уравнений Максвелла в дифференциальной форме:

.

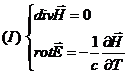
Рассмотрим первое уравнение первой пары. Проинтегрировав его по объему, получим выражение

.

Согласно теореме Остроградского-Гаусса, это можно переписать как

.

Выражение есть элементарный поток вектора напряженности 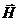. Тогда 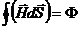есть полный поток вектора 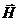, причем из уравнения . То есть, можно сказать, что полный поток вектора 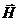через замкнутую поверхность равен нулю.

Иногда поток характеризуют в терминах числа линий напряженности. Для этого каждой линии напряженности необходимо сопоставить элементарный магнитный поток, и тогда полный поток будет представлять собой

,

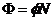где 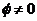– элементарный магнитный поток, 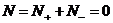, то есть линии напряженности нигде внутри объема не обрываются и не появляются. Кстати, отсюда можно сделать вывод о том, что магнитных зарядов не существует.

Так как каждой магнитной линии сопоставляется элементарный магнитный поток, возникает идея об определении его величины. Однако, прежде следует рассмотреть второе уравнение первой пары уравнений Максвелла:

.

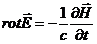Проинтегрировав его по некоторой незамкнутой поверхности, получим

.

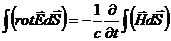Следует отметить, что не важно, брать здесь частную или полную производную по времени, так как после интегрирования останется только временная зависимость.

.

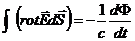Применив теорему Стокса, здесь можно перейти от интеграла по поверхности к интегралу по замкнутому контуру:

.

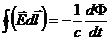Если теперь домножить левую часть на единичный заряд, то получим

,

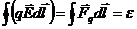где 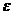- работа по перемещению единичного положительного заряда по замкнутому контуру (ЭДС). Окончательно можно записать

.

Формально, это означает, что при любом изменении магнитного потока, пронизывающего замкнутый контур, в этом контуре возникает ЭДС. Согласно закону электромагнитной индукции Фарадея, ЭДС имеет такое направление, что своим собственным магнитным полем препятствует изменению магнитного потока, вызвавшему этот ток.

В данном случае электрический ток возникает без источника тока.

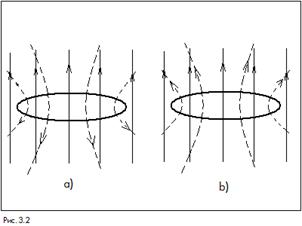
Рассмотрим сначала случай, когда поток увеличивается (рис. 3.2, а)), то есть

.

Согласно закона Фарадея необходимо возникнет ЭДС, которая создаст ток, препятствующий увеличению магнитного потока (иначе: по правилу "буравчика"). В свою очередь ток создаст собственное магнитное поле, силовые линии которого будут искривлены и направлены "навстречу" магнитному полю, вызвавшему этот ток.

Если теперь поток убывает (рис. 3.2, b)), то есть

,

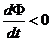то ЭДС будет вызывать ток, препятствующий уменьшению потока. Сонаправленные поля складываются.

Если подбирать колеблющийся поток, то можно подобрать его так, чтобы кольцо с током вибрировало или вообще находилось в подвешенном состоянии.

Вернемся теперь к рассмотрению элементарного магнитного потока 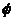, который еще иногда называют квантом магнитного потока. Запишем второе уравнение первой пары уравнений Максвелла:

,

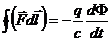где теперь 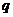не обязательно единичный заряд. Проинтегрировав обе части по , получаем выражение

.

Известно, что – импульс. Таким образом получили

.

Согласно правила квантования Бора, этот интеграл кратен целому числу постоянных Планка :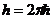

.

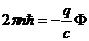Отсюда следует, что магнитный поток квантуется:

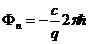
и его минимальное значение при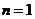

.

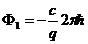Очевидно, что элементарный магнитный поток величина положительная, так как заряд электрона .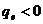

На самом деле, элементарный магнитный поток может быть найден и экспериментально. В частности достаточно точными являются эксперименты со сверхпроводящими кольцами. Известно, что сверхпроводники являются идеальными диамагнетиками, так как совершенно "не пропускают" внутрь себя магнитное поле.

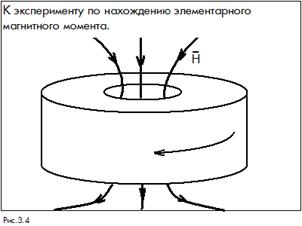
Под действие внешнего поля в кольце из сверхпроводника возникают токи, "противодействующие" полю (рис. 3.3.). После "выключения" внешнего поля за счет явления сверхпроводимости ток все равно будет течь, порождая собственное магнитное поле (рис. 3.4.). Если теперь вновь "включить" внешнее поле, но уже меньшее, чем первоначальное, то собственное поле кольца также будет меньше и магнитный поток уменьшится. Возникает вопрос: до какой степени можно уменьшать внешнее магнитное поле так, чтобы это вызывало дальнейшее уменьшение магнитного потока?

Когда в эксперименте внешнее магнитное стало мало, то собственное поле кольца стало изменяться ступенчато, дискретно (рис. 3.5.). наконец, было получено минимальное значение магнитного потока, которое соответствовало элементарному магнитному потоку 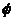. Отметим, что измеренное значение 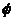в точности совпало с теоретически полученным значением элементарного потока.

Следует отметить, что в сверхпроводниках носителями тока являются спаренные электроны, то есть

.

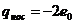Тогда отсюда получим для элементарного магнитного потока

.

В эксперимент было получено точно это значение.

Этот эксперимент также подтвердил тот факт, что носителями тока в сверхпроводниках являются спаренные электроны.

Не нашли, что искали? Воспользуйтесь поиском: