Четырехмерный вектор плотности тока.

Проблема состоит в том, что в рамках теории поля понятия точечного заряда или заряженной частицы не существует. В ней все физические величины в некотором смысле рассредоточены в пространстве. Но так как объективно понятие точечного заряда существует, необходимо разработать специальный математический аппарат для их описания применительно к теории поля.

"Размажем" заряд по пространству и введем внутри этой области радиус-вектор, который определяет плотность заряда в некоторой точке:

.

Этот вектор не удобен для описания, поэтому введем неподвижное начало координат "0", из которого восстановим два вектора и .

Эти три вектора связаны соотношением:

.

Тогда плотность заряда будет зависеть от разности . Но на данном этапе точечный заряд не определен. Чтобы его ввести необходимо представить плотность заряда в виде

.

Так как дельта-функция имеет пик в области 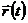, весь заряд по сути собран в одной точке. В этом случае можно записать

,

то есть заряд эквивалентен точечному, но находится "во всем" пространстве. Дельта-функция "отслеживает" траекторию частицы, а, следовательно, и движение точки, описываемой .

Аналогичным образом введем трехмерный вектор плотности тока:

,

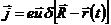где – фактическая скорость частиц.

Соответственно,

.

Введем четырехмерный вектор плотности тока следующим образом:

.

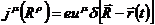Следует иметь в виду тот факт, что не является четырехмерным вектором. Однако, является четырехмерным вектором, так как выше указанная дельта-функция неинвариатна (таким образом, получено нековариантное представление четырехмерного вектора плотности тока).

Более удобным является представление четырехмерного вектора плотности тока в явно ковариантной форме:

.

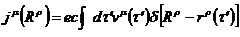Здесь – инвариантный параметр, который, как будет показано позже, перейдет в собственное время.

Теперь следует убедиться, что полученное определение совпадает с полученным ранее. Перепишем его, выделив временную часть дельта-функции:

.

Необходимо снять интегрирование по , воспользовавшись для этого правилом интегрирования дельта-функции от сложного аргумента (дельта-функцию от сложного аргумента можно представить как

),

где 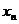– корень уравнения .

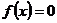В нашем случае зависимость от однозначна, и, положив в производной 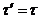– корень этого уравнения – можно записать:

.

Снимая интегрирование по и учитывая тот факт, что , имеем

,

где 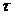– собственное время.

Данное выражение совпадает с тем, что было получено для нековариантного определения тока. Несложно убедиться в том, что уравнение непрерывности , где , также выполняется.

Не нашли, что искали? Воспользуйтесь поиском: