Закон сохранения плотности энергии-импульса в дифференциальной форме.

Известно, что плотность силы можно определить следующим образом:

– для частицы.

Но эту же величину можно записать как

– для поля.

Следовательно, получаем закон:

–

закон сохранения энергии-импульса в дифференциальной форме.

Покажем теперь, что из этого закона можно получить силу, которая действует на заряд в электромагнитном поле – силу Лоренца. Распишем плотность силы для частицы и для поля:

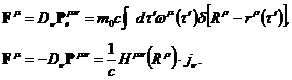
Подставим четырехмерный вектор плотности тока в интегральной форме в выражение для плотности силы для поля:

.

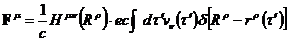Теперь можно записать закон сохранения в виде

.

Нулю равно выражение в фигурных скобках, так как дельта-функция не является тождественно равной нулю. Таким образом, можно записать, что

,

то есть получена сила Лоренца.

Чтобы теперь перейти от теории поля к теории частиц, необходимо проинтегрировать по четырехмерному объему :

.

Здесь интегрирование по снято. Силу Лоренца можно обозначить как 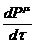, а . Так как внешнее поле от не зависит, то интеграл по 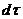можно снять:

.

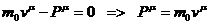Получено выражение для четырехмерного вектора импульса. Значит выражение для закона сохранения энергии-импульса в дифференциальной форме верно.

Заметим, что в наиболее общем виде закон сохранения энергии-импульса записывается следующим образом:

.

В итоге получается уравнение движения с учетом радиационного трения (замедление движения за счет излучения).

Вектор Пойнтинга.

Начнем рассмотрение отдельных компонент тензора плотности энергии-импульса с рассмотрения пространственно-временной компоненты . Запишем:

.

Для того, чтобы получить вектор Пойнтинга, проведем суммирование по , положив :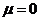

.

Перепишем это выражение следующим образом:

.

Проинтегрируем по , применив в первом слагаемом теорему Остроградского-Гаусса:

,

где – энергия электромагнитного поля. Получаем:

–

закон сохранения энергии системы, состоящей из частиц и полей. Таким образом, физический смысл вектора Пойнтинга – поток энергии электромагнитного поля. – энергия поля, проходящая в единицу времени через единицу площади нормально к ней. Тогда мощность излучения системы можно записать как

.

Таким образом, если , то потоки энергии нет, и получим, что

.

Система ведет себя как консервативная и

.

Не нашли, что искали? Воспользуйтесь поиском: