Об устойчивости статической системы электрических зарядов.

Простейший случай одноименных зарядов является неустойчивой системой, так как они будут отталкиваться друг от друга с кулоновской силой

.

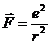Разноименные заряды будут притягиваться друг к другу и в конце концов упадут друг на друга.

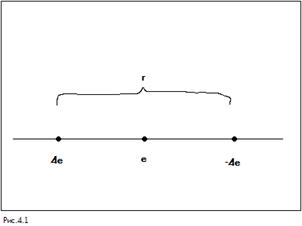
Рассмотрим расположение трех зарядов, изображенное на рис.4.1. Эта система квазиустойчива. Для устойчивого положения сила отталкивания должна компенсировать силу притяжения:

.

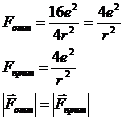Однако, эта система неустойчива, так как равенство справедливо только для стационарного состояния. Если же один из зарядов сместить, то система выйдет из состояния равновесия, в которое уже не вернется.

По этому поводу существует теорема Ирншоу, которая гласит, что существование устойчивой стационарной системы зарядов невозможно.

Идея доказательства состоит в нахождении потенциальной энергии системы и доказательстве того, что она не имеем минимума, откуда и следует неустойчивость системы.

Действительно, энергия системы может быть найдена как

.

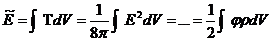Для системы электростатических зарядов

.

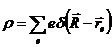Тогда энергия запишется как

.

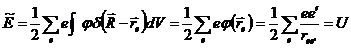Для того, чтобы энергия системы имела минимум, необходимо, во-первых, чтобы все первые производные по координатам зарядов были равны нулю и, во-вторых, все вторые производные от потенциальной энергии были положительными.

Оказывается, что сумма всех вторых производных равняется нулю:

,

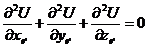что автоматически означает отсутствие минимума потенциальной энергии. докажем, что это соотношение имеет место.

Рассмотрим сначала ситуацию, когда 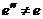и 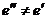. Тогда производные берутся по "чужим" переменным и они всегда дают нуль.

В случае, когда 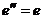или 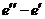, тогда

.

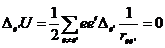Следовательно, вышеуказанное равенство действительно имеет место и минимума потенциальной энергии нет – существование устойчивой системы невозможно.

Не нашли, что искали? Воспользуйтесь поиском: