Орбитальный и спиновый угловые моменты электромагнитного поля.

Перейдем от плотности углового момента к самому угловому моменту. С этой целью в дифференциальном законе распределения углового момента перейдем от интегрирования по четырехмерному объему к интегрированию по замкнутой гиперповерхности (теорема Остроградского-Гаусса):

.

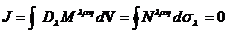Выберем гиперповерхность в виде гиперкуба (на рис.3.13. изображена проекция " "-сечения этого куба). Для этой гиперповерхности можно записать, что

,

где . Проведя интегрирование по столь простой поверхности, получим выражение

.

Будем считать, что электромагнитное поле имеет островной характер и обращается в нуль на пространственной бесконечности. Устремим пространственные грани гиперкуба на бесконечность. На гранях поля нет и поэтому справедливым будет записать

или .

Так как грани куба были выбраны произвольно, то же выражение можно записать как

–

закон сохранения полного углового момента.

В итоге:

.

Закон сохранения орбитального момента:

.

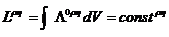Закон сохранения спинового момента:

.

Рассмотрим отдельно компоненты этих тензоров.

Для орбитального момента зададим:

.

Плотность углового момента равна . Формула плотности углового момента совпадает с формулой углового момента в механике с той лишь разницей, что в формуле для плотности углового момента для поля фигурирует плотность импульса.

Рассмотрим пространственно-временную компоненту орбитального момента:

,

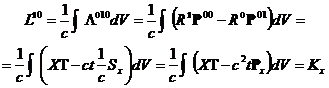где

,

а в свою очередь – плотность компонент .

Таким образом все компоненты орбитального момента найдены:

.

Введем радиус-вектор центра инерции системы электромагнитного поля:

.

Тогда получим для :

.

Так как

,

для производной имеем выражение

.

Рассмотрим теперь спиновые свойства электромагнитного поля:

,

где

.

Найдем пространственные компоненты :

.

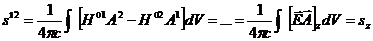Обобщив, получим выражение

–

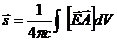спин электромагнитного поля.

Введя спин, можно ввести и плотность спина в виде

.

Найдем пространственно-временные компоненты:

.

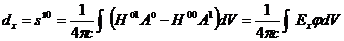И, следовательно, обобщая, получим выражение

.

Тогда полностью найденные компоненты выглядят как

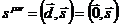
и, соответственно,

.

Равенство нулю нуль-компоненты обусловлено тем фактом, что потенциалы всегда можно нормировать.

Рассмотрим теперь еще более конкретный пример плоской монохроматической волны с круговой поляризацией. В каждой точке пространства с радиус-вектором , через которую проходит эта волна, имеют место колебания напряженностей электромагнитного поля следующего типа:

,

где . Положительное значение отвечает правой поляризации, отрицательное – левой. С другой стороны

.

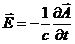Значит, векторный потенциал в данной точке также будет испытывать колебания вида

.

Очевидно имеем

,

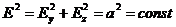стало быть плотность энергии будет равна

.

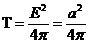Волна распространяется вдоль единичного вектора . Плотность орбитального момента определяется выражением

,

а сам орбитальный момент –

.

Плотность пространственно-временных компонент определяется выражением

.

Сами пространственно-временные компоненты определяются как

.

Таким образом можно записать, что

.

У плоской монохроматической волны нет орбитального момента.

Плотность спинового момента определяется соотношением

.

Иначе говоря,

.

Тогда выражение для спина запишется как

,

где – энергия электромагнитной волны.

Не нашли, что искали? Воспользуйтесь поиском: