Законы сохранения в дифференциальной форме как следствие однородности и изотропности пространства.

П.п.1. Вариация действия в теории поля.

В релятивистской механике математическая идея ввода законов сохранения состояла в следующем:

.

При преобразованиях координат функция действия изменяется. Если преобразования координат являются бесконечно малыми, то можно найти соответствующую вариацию действия, которая отвечает повороту и/или трансляции системы координат:

.

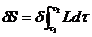Для изохронных преобразований:

,

так как для любого момента времени 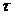должно выполняться условие 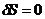, а значит и 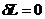. Это и является ключевым моментом в определении законов сохранения в релятивистской механике. Истинная траектория только одна, а все остальные траектории, отличающиеся от истинной, образуют множество виртуальных траекторий. Отсюда: мы имеем право положить 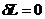для какого-то произвольного момента времени. В теории поля мы заменяем функцию Лагранжа плотностью функции Лагранжа:

,

а соответствующие законы сохранения получаем исходя из того, что

.

В теории поля нет собственного времени, а значит необходимо варьировать не только координаты, но и сами функции, от которых зависит плотность функции Лагранжа. Более того, так как действие в таком поле определяется как

,

вариация действия будет иметь вид

.

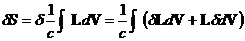Вариация функции поля состоит из двух принципиально различных частей: из вариации формы (вида) функции и вариации, связанной с изменением аргумента функции. Так при преобразовании координат некоторая функция перейдет в . Если вариация мала, то вариация будет состоять из двух частей:

,

где – вариация формы функции, – тейлоровская добавка за счет изменения аргумента.

Рассмотрим первое свойство вариации формы функции. Оказывается, что если взять производную от вариации формы функции, то операции взятия вариации и взятия производной можно менять местами:

.

Это несложно показать:

–

что и требовалось показать.

Также можно показать, что вариация от четырехмерного объема имеет вид:

.

Действительно,

,

где – якобиан перехода, который выглядит как

,

где в свою очередь . Взяв эту производную, можно найти якобиан:

.

Тогда вариация от четырехмерного объема имеет вид

.

Запишем вариацию действия:

.

Вычислим отдельно

.

Тогда окончательно для вариации действия имеем

.

Необходимо равенство вариации действия нулю, так как уравнения движения не должны зависеть от преобразований координат.

П.п.2. Закон сохранения тензора плотности энергии-импульса в дифференциальной форме как следствие однородности и изотропности пространства.

Будем считать, система координат не движется, а движется некоторая кривая, описывающая изменение некоторой функции . Все ее точки сдвигаются на один и тот же отрезок:

.

Но с другой стороны

.

Таким образом, вариация формы равна

.

Подставим полученное в формулу для вариации действия:

.

То, что стоит в фигурных скобках можно обозначить за – плотность энергии-импульса. Эта величина совпадает с тензором плотности энергии-импульса чистого электромагнитного поля. Запишем:

.

Чтобы интеграл в определении вариации действия всегда равнялся нулю необходимо, чтобы подынтегральное выражение обращалось в нуль при любых преобразованиях координат, то есть

.

Это закон сохранения плотности энергии-импульса чистого электромагнитного поля в дифференциальной форме. Следует теперь вычислить этот тензор и убедиться, что он совпадает с выражением, которое было получено ранее.

Плотность функции Лагранжа для чистого поля выглядит как

,

как это было показано в параграфе 3.3.

Тогда тензор плотности энергии-импульса будет иметь вид

.

Добавка при подстановке в дифференциальный закон сохранения даст нуль. В конечном итоге имеем:

.

Убедимся, что при подстановке даст нуль:

.

Первый и второй члены равны нулю, так как тензор антисимметричен, а следовательно, конструкция автоматически равняется нулю.

П.п.3. Закон сохранения тензора плотности углового момента чистого электромагнитного поля в дифференциальной форме как следствие изотропности пространства и времени.

Рассмотрим вариацию действия для электромагнитного поля в общем случае:

,

где . Вариация формы выглядит как . В отличии от трансляции здесь полная вариация уже не будет равной нулю. Таким образом, в итоге для вариации действия можно записать (выражение в фигурных скобках)

.

Полная вариация потенциала связана с преобразованием поворота осей координат. Для преобразований поворота и трансляции:

,

.

Подставляем в фигурные скобки в выражении для вариации действия:

,

где 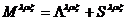– тензор плотности углового момента, – тензор плотности углового орбитального момента, – тензор плотности спинового момента.

Запишем теперь вариацию действия целиком:

.

Так как , то необходимо выполняется . Опять же, так как при поворотах , имеем .

Этот закон сохранения распадается на два независимых закона сохранения:

.

Докажем один из этих законов:

.

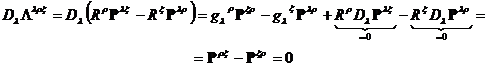Не нашли, что искали? Воспользуйтесь поиском: