ТЕОРИЯ ВЕРОЯТНОСТЕЙ

Теория вероятностей изучает закономерности для случайных явлений. Одним из основных терминов теории вероятностей является понятие случайного события. Событием называется всякий факт (исход), который в результате опыта (испытания, эксперимента) может произойти или не произойти. Каждому из таких событий можно поставить в соответствие определенное число, называемое его вероятностью, и являющееся мерой возможного совершения этого события. Например, отказ изделия - событие случайное, которое всегда имеет малую вероятность, если изделие обладает высокой эксплутационной надежностью.

Проведем классификацию основных типов событий. Совместные события – такие события, появление одного из которых не исключает возможности появления другого. Попарно несовместные события – такие события, появление одного из которых исключает любые возможности появления другого из остальных. Зависимые события – такие события, появление одного из которых влияет на появление другого события. Попарно независимые события – такие события, появление одного из которых не влияет на появление другого события из остальных. Противоположные события это такие два события и , для которых наступление любого из них приводит к тому, что другое событие не наступает. Например, наступает , а событие не наступает и, наоборот.

Полная группа событий – такое множество событий, в котором в результате опыта должно произойти хотя бы одно из событий этой группы событий. Противоположные события и составляют полную группу событий. Достоверное событие ­– это такое событие, которое обязательно происходит при проведении опыта. Невозможное событие – это такое событие, которое не может происходить при проведении опыта. Элементарное событие – это такое событие, которое не может быть расчленено на более мелкие части по отношению ко всем возможным результатам (исходам) проводимого опыта. Сложное событие – это такое событие, которое может быть расчленено на более мелкие события и является комбинацией элементарных событий. Наиболее удобные для

практики комбинации событий является сумма, либо произведение нескольких событий.

Сумма событий 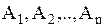– такое событие , которое описывается в данном опыте фактом появления хотя бы одного события из указанного элементного множества событий. Сумма событий (объединение) обозначается .

Произведение событий 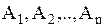-такое событие , которое описывается в данном опыте фактом наблюдения одновременного появления всех событий из указанного элементного множества событий. Произведение событий (пересечение) обозначается . Приведем теоремы сложения и умножения вероятностей. Теоремы сложения для совместных и несовместных событий имеют вид

,

Ø.

Теоремы умножения для зависимых и независимых в совокупности случайных событий

,

.

Символ Ø обозначает пустое множество. Последняя формула, приведенная в последней строчке, справедлива для независимых в совокупности событий. В случае двух событий,

которые независимы, условная вероятность и безусловная вероятности совпадают

.

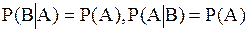Пусть событие может произойти в результате появления только одного события ,

входящего в полную группу попарно несовместных событий , тогда

справедлива формула полной вероятности, которая позволяет найти вероятность

.

Несовместные события из полной группы называются гипотезами, причем

.

Вероятности гипотез после проведения опыта уточняются формулой Бейеса

.

Классическое определение вероятности для события выражается отношением

,

где – число всех элементарных исходов, благоприятствующих появлению события ;

– общее число возможных элементарных исходов, которые образуют полную группу равновозможных событий. Относительная частота события равна отношению

,

где – число испытаний, в которых данное событие наступило; – общее число произведенных испытаний. Опыты считаются независимыми, если вероятность того или иного исхода каждого из них не зависит от того, какие исходы имели другие опыты. Для

схемы независимых испытаний справедлив биномиальный закон распределения вероятностей (формула Бернулли). Формула Бернулли позволяет найти вероятность того, что событие произойдет ровно раз при проведении независимых опытов

, ,

где – вероятность появления события в любом одном испытании, – число комбинаций в виде сочетаний из по элементов. Комбинация в виде сочетания из по элементов представляет собой подмножество, состоящее ровно из разных элементов. Такое подмножество принадлежит заданному – элементному множеству. Сочетание от другого сочетания отличается хотя бы одним элементом.

Комбинация в виде размещения из по элементов представляет собой набор, состоящий ровно из разных элементов. Такой набор принадлежит заданному – элементному множеству. Размещение от другого размещения отличается либо составом элементов, либо порядком следования элементов. Число комбинаций в виде размещения из по элементов находится по формуле

.

В случае размещения превращаются в другие комбинации–перестановки. Число

комбинаций в виде перестановок из элементов находится с помощью формулы

.

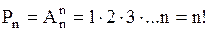Перестановка от другой перестановки отличается только порядком следования элементов.

Состав элементов в комбинации в виде перестановки остается постоянным.

Пример7. Классическое определение вероятности.

Из колоды в 36 карт наудачу извлекли три карты. Найти вероятность среди них окажется валет. Решение. Найдем значения числителя и знаменателя 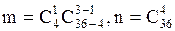, тогда . Ответ .

Пример 8. Теоремы сложения и умножения вероятностей.

На объекте работают три видеокамеры. Вероятности безотказной работы видеокамер разные, и равны соответственно . Найти вероятность того, что работает хотя

бы одна видеокамера этого объекта. Решение. Для суммы событий

. Ответ .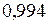

Не нашли, что искали? Воспользуйтесь поиском: