Теорема Абеля о структуре области сходимости степенного ряда.

Если степенной ряд сходится для некоторого значения х₀, не равного нулю, то он сходится абсолютно для всех значений х, для которых выполняется условие:

Если степенной ряд расходится для некоторого значения х₀, то он расходится для всех значений х, для которых выполняется условие:

Из теоремы Абеля вытекает, что для произвольного степенного ряда существует положительное число R (конечное или бесконечное), такое, что для всех ряд сходится абсолютно, а при ряд расходится.

Интервал , во всех точках которого степенной ряд сходится, а в точках, которые не принадлежат данному интервалу, степенной ряд расходится называется интервалом сходимости данного ряда.

Половина интервала сходимости называется радиусом сходимости степенного ряда. Если , то интервал сходимости составляет всю числовую ось . Если 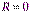, то степенной ряд сходится лишь при , то есть интервал сходимости вырождается в точку.

34.Отыскание радиуса сходимости степенного ряда по методу Д`Аламбера и Коши. Определение области сходимости степенного ряда. Обобщенный степенной ряд. Область сходимости обобщенного степенного ряда.

Областью сходимости степенного ряда называется множество тех значений х, при которых степенной ряд сходится.

Если степенной ряд сходится для некоторого значения х₀, не равного нулю, то он сходится абсолютно для всех значений х, для которых выполняется условие:

Если степенной ряд расходится для некоторого значения х₀, то он расходится для всех значений х, для которых выполняется условие:

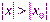
Теорема Абеля дает ясное представление о структуре области сходимости степенного ряда.

Область сходимости степенного ряда совпадает с одним из следующих интервалов:

1) ; 2) ; 3) ; 4) ,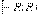

Где, R – некоторое неотрицательное действительное число или .

Число R называется радиусом сходимости, интервал – интервалом сходимости степенного ряда.

Радиус сходимости R степенного ряда можно найти по одной из следующих формул:

формула Даламбера:

формула Коши:

Если в формуле Коши , то полагают , если , то полагают .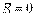

Ряд вида:

называется обобщенным степенным рядом. Интервал сходимости обобщенного степенного ряда:

То есть областью сходимости ряда является интервал

Не нашли, что искали? Воспользуйтесь поиском: