Ряды Тейлора и Маклорена для произвольной функции. Условие сходимости. Остаточный член ряда Тейлора. Его оценка в приближенных вычислениях.

Представление функции f(x) в виде ряда

называется разложением этой функции в ряд Тейлора.

Разложение функции f(x) в ряд Тейлора при x₀=0

называется разложением этой функции в ряд Маклорена.

Остаток ряда Тейлора (Маклорена) получается отбрасыванием от основных рядов n первых членов и обозначается как . Тогда функцию f(x) можно записать как сумму n первых членов ряда и остатка :

,

то есть

.

Абсолютная погрешность такого приближения равна модулю остаточного члена.

Необходимое и достаточное условие сходимости ряда Маклорена: Пусть радиус сходимости ряда 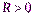. Для того, чтобы этот ряд сходился в интервале к функции f(x), необходимо и достаточно, чтобы выполнялось условие: в указанном интервале.

Если производные любого порядка функции f(x) в некотором промежутке ограниченны по абсолютной величине одним и тем же числом M, то есть 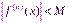, то в этом промежутке функцию f(x) можно разложить в ряд Маклорена.

Не нашли, что искали? Воспользуйтесь поиском: