Постановка задачи нелинейного программирования.

Лекция 4 Нелинейное программирование

1 Постановка и классификация задач нелинейного программирования

2 Методы решения задач нелинейного программирования

Постановка и классификация задач НЛП

Постановка задачи нелинейного программирования.

В классической теории оптимизации для нахождения точек максимума и минимума (экстремальных точек) целевой функции в условиях, как отсутствия, так и наличия ограничений на переменные, широко используется аппарат дифференциального исчисления. На использовании этого аппарата построено большинство алгоритмов решения задач нелинейного программирования.

Классическая задача нелинейного программирования ставится следующим образом:

Максимизировать (Минимизировать) целевую функцию f=f(x) при ограничениях g(x)=0, где x = (x₁, x₂, …, x_n), xÎR_n, g(x) = (g ₁(x), g ₂(x), …, g _m(x))^T.

Ограничения g(Ф) заданы в виде неравенств:

,

где b_i – число, ограничивающее i –й ресурс.

Данные задачи имеют экономическое приложение. Смысл задач состоит в том, что результаты деятельности предприятия растут непропорционально изменению масштаба ресурсов, т.к. есть процесс насыщения рынка.

Примеры

Потребитель располагает доходом в условных денежных единиц, который расходуется им на приобретение потребительского набора, состоящего из двух благ (продуктов). Обозначим – количество единиц первого блага, – второго; и – рыночные цены одной единицы первого и второго блага соответственно. На множестве потребительских наборов 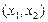определена индивидуальная функция полезности потребителя в виде степенной гиперболы. Построить математическую модель для определения оптимального потребительского набора.

Пусть . Целевая функция имеет вид

.

Рассмотрим задачу потребительского выбора (рационального поведения потребителя на рынке), которая заключается в выборе такого потребительского набора , который максимизирует его функцию полезности при заданном бюджетном ограничении (денежные расходы на блага не могут превышать денежного дохода).

С математической точки зрения задача потребительского выбора имеет вид: найти неотрицательные значения переменных , удовлетворяющих ограничению в виде неравенства и доставляющих максимум нелинейной целевой функции .

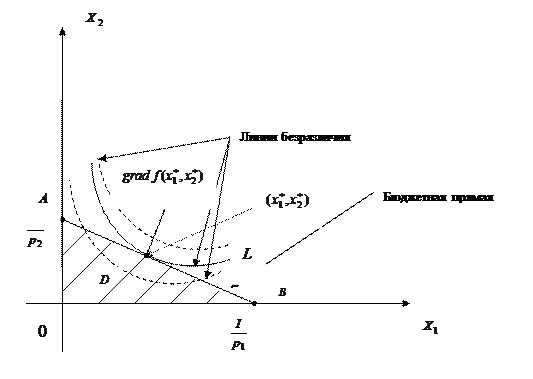
Данная модель является моделью НП, для решения которой применим алгоритм графо-аналитического метода для двух переменных. Для этого на плоскости в первой четверти построим бюджетную прямую или . Эта прямая разбивает плоскость на две полуплоскости. Выберем нужную полуплоскость в соответствии с ограничением, получим область – треугольник .

Построим линии уровня (линии безразличия), являющиеся степенными гиперболами. Отсюда видно, что максимум целевой функции достигается в точке – касания бюджетной прямой и линии безразличия .

Найдем решение задачи:

Решим данную задачу с помощью метода множителей Лагранжа.

Функция Лагранжа для нее имеет вид

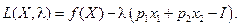
Необходимые условия существования экстремума имеют вид:

Исключая из данного уравнения множитель Лагранжа, получим

Решение данной системы называется решением задачи потребительского спроса.

В многомерном случае функция Лагранжа имеет вид:

Система уравнений имеет следующий вид:

.

Исключая из уравнений неизвестную, получим

Ответ. Оптимальный потребительский набор – точка касания линии безразличия и бюджетной прямой.

Пример.

Пусть функция полезности (в неоклассической постановке) имеет вид

Из первого уравнения следует, что затраты на оба вида товаров должны быть одинаковыми. . Оптимальное решение находится в точке с координатами .

Иными словами, в данном случае расход на каждый товар составляет половину дохода потребителя, а количество товаров каждого типа определяется его ценой.

Ограничения на область допустимых значений каждого x_iÎX_i могут быть заданы и могут отсутствовать. Функции f(x) и g _i (x) (i = 1, 2,..., т), в общем случае нелинейно зависят от своих аргументов, но предполагаются дважды непрерывно дифференцируемыми.

В ситуации, когда т<п, обычно стремятся выразить т переменных через остальные п – т переменных, а затем исключить их из числа элементов целевой функции, заменив эти т переменных их выражением через остальные п – т переменных. В этом случае задача нахождения условного экстремума превращается в задачу нахождения безусловного экстремума функции f(Z) = (j₁, …, j_n–m). Данный способ положен в основу нескольких методов решения задач нелинейного программирования: метода приведенного градиента (метода Якоби), метода исключения, метода множителей Лагранжа.

Наиболее разработан класс моделей нелинейного программирования для целевых функций, у которых точки локального экстремума являются оптимальными точками, то есть точками глобального экстремума. К ним относятся выпуклое и квадратичное программирование. Согласно локально-глобальной теореме локальный экстремум для таких задач является и глобальным.

Для задач НЛП нет единого метода решения задачи. Существуют методы множителей Лагранжа, квадратичное, выпуклое программирование, приближенные методы решения задачи, графоаналитический метод. Наиболее разработаны методы, в которых целевая функция нелинейная, а ограничения линейны. Однако даже для такого класса задач оптимальное решение может быть найдено только для определенного класса целевых функций.

Для классификации задач НЛП введем ряд дополнительных определений для их математического описания.

Определение. Функция называется сепарабельной, если она может быть представлена в виде суммы функций, каждая из которых является функцией одной переменной

.

Замечания

1. Классификация моделей НП связана с:

– видом целевой функции f (x), которая может быть линейной, квадратичной, выпуклой (вогнутой), сепарабельной или более сложной, кроме того, f (x) может быть одномерной или многомерной. Тогда модели НП называются линейными, квадратичными, выпуклыми, сепарабельными соответственно;

– видом функций ограничений, которые могут быть линейными и нелинейными разного вида и задаваться в виде равенств и неравенств.

2. В общем виде критерии нахождения оптимального решения для модели нелинейного программирования задаются теоремами Куна–Таккера.

3. Модель нелинейного программирования переходит в модель линейного программирования, если ограничения – – целевая функция – линейные функции.

Определение. Функция называется квадратичной, если она имеет вид:

,

где 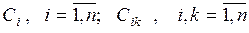– заданные числа.

Определение. Квадратичная форма называется отрицательно определенной, если

.

В противном случае квадратичная форма называется положительно определенной.

Модель квадратичного программирования (частный случай общей модели выпуклого программирования) используется в том случае, когда в исследуемой системе (объекте), целевая функция квадратичная и область допустимых решений D определяется линейными ограничениями.

С математической точки зрения общая модель квадратичного программирования задается следующим образом.

Найти неотрицательные значения переменных , удовлетворяющие линейным ограничениям

и доставляющие максимум целевой функции

,

где – отрицательно определенная квадратичная форма.

Задачей квадратичного программирования называется задача

При ограничениях

Преобразуем ограничения неравенства в ограничения равенства с помощью дополнительных переменных.

Для квадратичного программирования функция Лагранжа имеет вид

.

Определение. Задача нелинейного программирования называется задачей дробно-линейного программирования, если ее математическая постановка имеет вид.

Целевая функция:

Ограничения линейные и имеют вид:

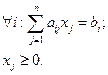
Примерами задач могут быть:

1. Задача определения рентабельности

Где - прибыль от единицы продукции -го вида;

- себестоимость производства единицы продукции -го вида;

2. Задача определения затрат в расчете на 1 рубль товарной продукции

Где цена единицы продукции -го вида;

- себестоимость производства единицы продукции -го вида;

3. Задача нахождения средней себестоимости

Где - затраты на производство единицы продукции -го вида;

Не нашли, что искали? Воспользуйтесь поиском: