Метод наискорейшего подъема

В зависимости от того, ищется максимум или минимум целевой функции, данный метод называется методом наискорейшего подъема или методом наискорейшего спуска. При использовании данного метода величина шага в итерационной формуле выбирается такой, чтобы обеспечить минимум f (X) в направлении, задаваемом вектором градиента, за 1 шаг. Для этого на каждом шаге по формуле

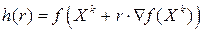
строится функция одной переменной r. Затем ищется экстремум функции 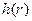любым удобным методом и определяется оптимальное значение переменной . Для поиска можно использовать любой удобный метод, одномерного оптимального поиска. После этого определяется величина градиента .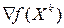

Если градиент равен нулю или достаточно мал, вычисления прекращаются, стационарная точка найдена. Далее эта точка проверяется на оптимальность. Если градиент больше заданной величины, необходимо вновь обратиться к формуле.

Пример 2. Найти максимум функции . Зададимся предельно допустимой величиной градиента в точке оптимума равной 0,125 по каждой координате. Найдем градиент функции , .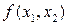

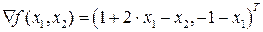Шаг 1. В качестве точки начального приближения выберем точку 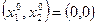. Подставив эту точку в формулу для вычисления градиента, получим, 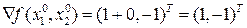. Градиент больше допустимого, следовательно, точка начального приближения находится достаточно далеко от экстремальной точки. Найдем функцию ,

.

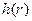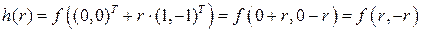Таким образом, 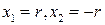. Подставив эти значения переменных 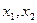в функцию 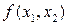, получим,

.

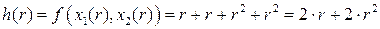Возьмем производную функции 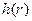и приравняем ее к нулю: 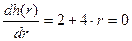. Отсюда получим значение переменной r, доставляющее максимум функции , .

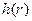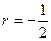По итерационной формуле найдем координаты точки первого приближения : .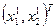

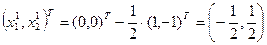Вычислим градиент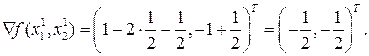

Величина градиента больше допустимой, необходимо продолжать поиск экстремальной точки.

Шаг 2. Выполнив действия аналогичные действиям шага 1, получим:

.

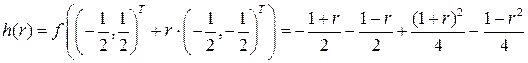Упростим данное выражение, 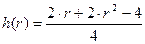, возьмем его производную и приравняем ее к нулю, 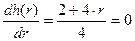. Следовательно, 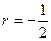. Найдем координаты точки 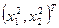, 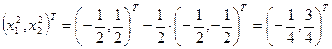. Затем найдем градиент функции в точке 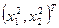. Получим, 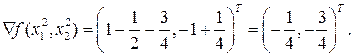градиент больше допустимого, продолжаем итерации.

Шаг 3. Действуя аналогично тому, как и на первых двух шагах, получим:

, , , ,

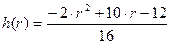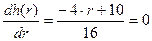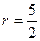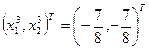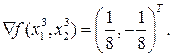
В результате третьей итерации градиент оказался равным допустимому. Следовательно, точка 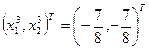находится достаточно близко к экстремальной и итерации необходимо закончить. На самом деле экстремум находится в точке с координатами 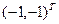С помощью матрицы вторых производных можно показать, что данная точка является точкой максимума.

Случайный поиск

Один из существенных недостатков методов, рассмотренных ранее, заключается в необходимости на каждом шаге вычислять градиент. Кроме того, в методе Ньютона-Рафсона на каждом шаге необходимо вычислять матрицу вторых производных и матрицу обратную по отношению к ней. В методе наискорейшего подъема на каждом шаге необходимо вычислять экстремум функции одной переменной 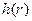. Этих недостатков лишены методы случайного поиска.

Основная особенность методов случайного поиска заключается в том, что направление движения на каждом шаге задается случайным образом. Один из наиболее часто применяемых приемов выбора направления движения заключается в следующем. Пусть ищется максимум функции f (X). В качестве точки начального приближения выбрана точка . Из этой точки в произвольном направлении делается пробный шаг длиной 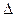. В полученной таким образом точке 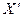замеряется значение функции f (X).

Если в новой точке значение функции окажется выше, чем в точке начального приближения, 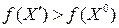, то направление от к 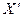признается подходящим для одномерного поиска. При этом длина шага может быть выбрана по любому известному правилу, например, по правилу продвижения до экстремума по выбранному направлению, как в методе наискорейшего подъема, или по случайному закону с известной функцией распределения.

Если значение функции в новой точке окажется ниже, чем в точке начального приближения, 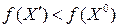, то подходящим признается противоположное направление.

Критерием остановки вычислений может быть неоднократное выполнение условия 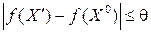, где 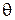- достаточно малое число. Кратность выполнения данного условия зависит от требуемой точности и надежности оценки и определяется с помощью методов математической статистики.

Не нашли, что искали? Воспользуйтесь поиском: