Графоаналитический метод решения задачи

К сожалению, в отличие от линейного программирования для задач НЛП нет универсального метода решения задачи. Наиболее разработаны задачи, для которых целевая функция нелинейная, а ограничения являются линейными и образуют многогранник области возможных решений. Однако оптимальное решение для таких задач может быть не только в вершинах многогранника на границах ОДЗ, но и внутри области или на его гранях.

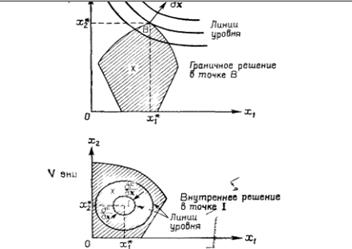
Геометрическое решение задач нелинейного программирования возможно и очень наглядно, когда количество аргументов целевой функции не превышает двух. В противном случае геометрические построения пришлось бы строить в n-мерном пространстве (n > 3), что является практически не реализуемым и совсем не наглядным.

Для реализации графоаналитического метода решения задач НП аналогично графоаналитическому методу реализации модели ЛП необходимо:

1. Найти область допустимых решений :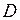

– на плоскости 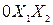построить прямые и кривые, уравнения которых получаются в результате замены в ограничениях на переменные знаков неравенств на знаки точных равенств;

– найти части плоскости , определяемые каждым из ограничений с учетом знаков неравенств;

– выделить область допустимых решений .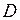

2. Построить в области допустимых решений 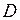линию уровня

.

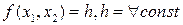3. Определить линию наивысшего уровня и найти точку 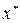в области 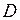, через которую она проходит (для поиска максимума целевой функции); для поиска минимума – определить точку 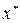области 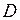, через которую проходит линия низшего уровня.

4. Определить координаты точки экстремума 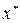(максимума или минимума) целевой функции, то есть оптимальное решение .

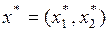5. Вычислить значение целевой функции 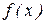в точке 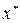, (или ).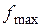

Рассмотрим несколько задач, в которых существуют линейные ограничения или линейная целевая функция. А также рассмотрим задачу, в которой и ограничения, и целевая функция нелинейные.

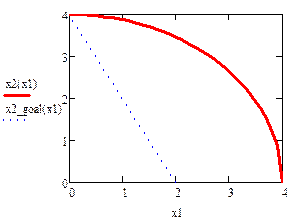
Пример 1. Линейная целевая функция и нелинейные ограничения

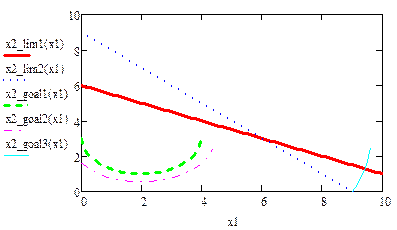
Область допустимых решений – часть круга радиуса 4. Линия уровня – прямая с угловым коэффициентом равным -2. Глобальный минимум находится в точке (0,0), а глобальный максимум – в точке, являющейся решением системы уравнений

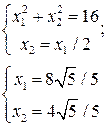
Пример Нелинейная целевая функция и линейные ограничения

Найти экстремумы функции

Минимальное решение находится в точке (2,3), а максимальное решение – в точке (9,0). Максимум равен 58, а минимум равен нулю.

Пример Нелинейная целевая функция и нелинейные ограничения.

Найти глобальные экстремумы функции

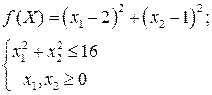
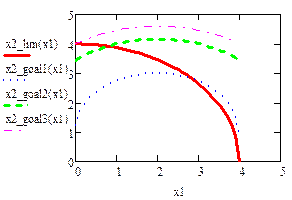
Глобальный максимум находится в точке (0,4). Он равен 13. Глобальный минимум находится в точке (0,0). Он равен нулю.

Пример: Требуется найти минимум целевой функции: W(X) = (x₁ – 2)² + (x₂ – 1)², при ограничениях: g(X) = x₁² – x₂ + 2 = 0.

Решение:

1. Построим на плоскости с осями координат x₁, x₂ параболу, заданную уравнением функции ограничения: x₂ =x₁² + 2. Эта парабола проходит через точки плоскости: (0, 0), (1, 3), (–1, 3), (2, 6), (–2, 6), (3, 11), (–3, 11). По данным точкам построим график функции. Эта парабола является пересечением поверхности допустимых значений f(X) и плоскости с осями координат x₁, x₂. Поверхность допустимых значений f(X) перпендикулярна плоскости x₁, x₂.

2. Выясним, какой геометрической фигурой является целевая функция f(X) = (x₁ – 2)² + (x₂ – 1)².

Из геометрии известно, что x ²+ y ²=R² есть уравнение окружности с радиусом R и центром в начале координат. В нашем случае таких окружностей можно построить бесконечное множество (в зависимости от значений радиуса). Самая маленькая из этих окружностей является точкой на плоскости x₁, x₂ с координатами (2,1). Радиус этой окружности R=0. Множество таких окружностей образует поверхность конуса, перпендикулярного плоскости x₁, x₂ и имеющего с ней одну общую точку (2, 1).

3. Поскольку минимальное значение целевой функции соответствует минимальному расстоянию между поверхностью конуса и плоскостью x₁, x₂, то при отсутствии ограничений это значение было бы достигнуто в точке (2, 1). Но при данном ограничении минимальное значение целевой функции должно принадлежать как поверхности конуса f(X) = (x₁ – 2)² + (x₂ – 1)², так и поверхности допустимых значений f(X), пересечением которой с плоскостью x₁, x₂ является парабола g(X) = x₁² – x₂ + 2 = 0. Как видно на графиках (рис.), эта точка имеет координаты x₁⁰» 0,55 x₂⁰»2,31, а целевая функция в этой точке принимает значение: f(X⁰)=(0,55 – 2)²+(2,31 – 1)²»3,8.

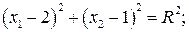
Рис.. Графики целевой функции и ограничения

2. В модели заданы целевая функция 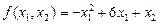и следующая система ограничений:

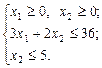
Найти максимум заданной целевой функции модели.

Решение. Данная модель является моделью нелинейного программирования, так как целевая функция нелинейна. Неизвестных две: и 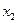. Поэтому для решения можно применить графоаналитический метод.

1. На плоскости построим прямые, уравнения которых получаются в результате замены в ограничениях на переменные знаков неравенств на знаки точных равенств, для удобства построения уравнение прямой приведем к виду прямой в отрезках: .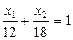

2. Найдем части плоскости , определяемые каждым из ограничений с учетом знаков неравенств.

3. Построим область допустимых решений 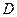(рис.).

4. Построим линии уровня. Покажем, что они представляют собой параболы.

;

;

.

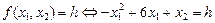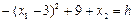
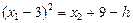Линии уровня – параболы (канонические уравнения с осью симметрии 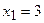, ветви направлены вверх. В зависимости от 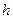парабола будет перемещаться вдоль оси симметрии.

5. Определим линию наивысшего уровня, так как ищем максимум. Очевидно, что это будет парабола, полученная перемещением вдоль оси симметрии вверх и касающаяся точки выхода из области 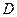, т.е. .

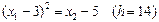Определим градиент 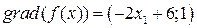. В точке x1=3 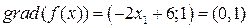. Направление градиента – вверх.

6. Найдем оптимальное решение задачи – координаты точки максимума – точки K - .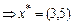

7. Вычислим значение целевой функции в точке – .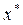

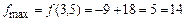Ответ. Максимальное значение целевой функции .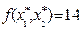

Не нашли, что искали? Воспользуйтесь поиском: