Если данная функция имеет седловую точку, то в ней выполняются условия Куна-Таккера.

Введя дополнительные переменные для преобразования неравенств условий Куна-Таккера в равенства, получим:

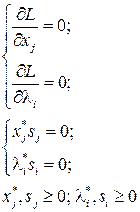
Для решения задачи квадратичного программирования необходимо решить систему алгебраических уравнений, удовлетворяющую условиям двойственности.

Решим задачу квадратичного программирования:

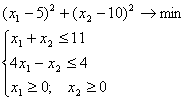
Решение.

Графическое решение задачи следующее:

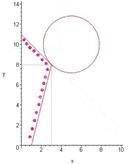
Система неравенств определяет область, ограниченную двумя прямыми и координатными осями. График целевой функции представляет собой окружность переменного радиуса с центром в точке (5, 10). Значение целевой функции графически представляет собой квадрат радиуса этой окружности. Минимальным радиусом, удовлетворяющим системе ограничений, будет такой радиус, который обеспечивает касание окружности с границей области так, как это показано на рисунке.

Искомая точка определяется как решение системы уравнений

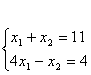
Получаем точку (3, 8), значение целевой функции в этой точке равно 8.

Теперь запишем задачу в традиционном виде:

Функция 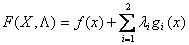называется функцией Лагранжа, а переменные 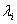- коэффициентами Лагранжа.

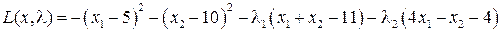
Условия Куна-Таккера

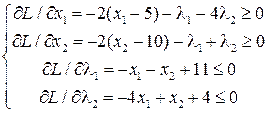
Найдя значения 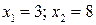получим

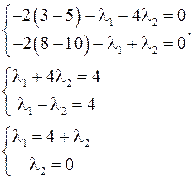
Пример.

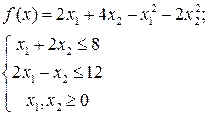
Функция вогнутая, т.к. представляет собой линейную, которую можно рассматривать как вогнутую и отрицательно определенную квадратичную.

Составим функцию Лагранжа

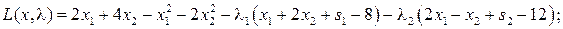
Запишем условия Куна-Таккера

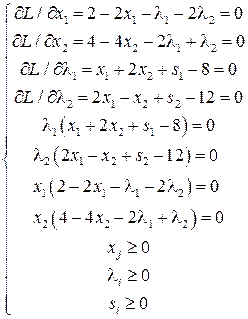
Не нашли, что искали? Воспользуйтесь поиском: