Обобщенный метод множителей Лагранжа

Метод множителей Лагранжа может быть обобщен на случай задачи с ограничениями в виде неравенств. Пусть дана задача:

,

.

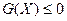Точка безусловного максимума функции f (X) может находиться внутри области ограниченной неравенствами, на границе этой области, либо вне ее. В первом случае условный и безусловный максимумы совпадают и находятся из уравнения . Во втором и третьем случаях условный максимум находится на границе области допустимых решений, превращая одно или несколько неравенств в равенства. С учетом вышеизложенного, алгоритм обобщенного метода множителей Лагранжа записывается следующим образом.

Шаг 1. Найти максимум функции f (X) без учета ограничений в виде неравенств. Если точка полученного максимума находится внутри области, сформированной данными ограничениями, закончить вычисления. Задача решена. В противном случае, положить k =1 и перейти к шагу 2.

Шаг 2. Сделать любые k ограничений активными (превратить их в равенства) и найти максимум целевой функции при наличии k активных ограничений методом множителей Лагранжа. Если полученное решение оказывается допустимым для остальных (m-k) ограничений системы, прекратить вычисления. Задача решена. В противном случае превратить в равенства другие k ограничений и повторить данный шаг. Если ни одно подмножество, состоящее из k активных ограничений, не привело к допустимому решению, перейти к шагу 3.

Шаг 3. При k=m прекратить вычисления. Задача решений не имеет. При k<m увеличить k на 1 и перейти к шагу 2.

Пример. Найти максимум функции 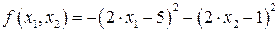при ограничениях , .

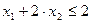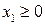Найдем безусловный минимум функции :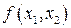

,

.

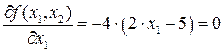Решив эти два линейных уравнения, получим: , 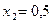. Полученная точка не удовлетворяет первому неравенству, так как 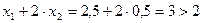. Сделаем активным второе неравенство: 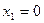. Сформируем функцию Лагранжа

.

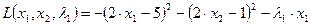Возьмем производные функции Лагранжа по всем переменным. Получим:

,

,

.

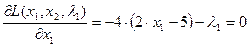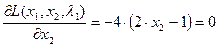Решив эту систему, получим: 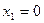, 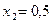. Поскольку 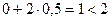, и обе переменные удовлетворяют условиям не отрицательности, задача решена. Оптимальное значение переменных, , .

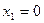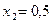Не нашли, что искали? Воспользуйтесь поиском: