Метод Ньютона - Рафсона

В методе Ньютона-Рафсона выбор длины шага на каждой итерации зависит от величины градиента. Чем больше градиент, тем длиннее шаг. Основанием для такого выбора длины шага служит предположение о том, что чем больше градиент функции в точке , тем длиннее интервал, в котором функция будет возрастать. Соответственно, чем больше по абсолютной величине отрицательный градиент, тем длиннее интервал, в котором функция будет убывать. Следовательно, метод Ньютона-Рафсона целесообразно использовать при поиске экстремумов достаточно гладких функций. Перейдем к изложению метода.

Как известно, необходимым условием экстремума функции f (X) в точке является равенство нулю всех ее первых производных:

, i =1.. n.

Разложив функцию в точке в ряд Тейлора, и ограничившись первыми двумя членами разложения, получим:

.

Обозначим: . Тогда

.

Матрица вторых производных функции - матрица является, во-первых квадратной, а во вторых – невырожденной. С учетом новых обозначений, система уравнений, может быть записана в матричной форме:

.

Умножив слева на , получим:

.

Оставив X в левой части приближенного равенства и перенеся все остальное в правую часть, получим:

Равенство является приближенным. Поэтому точка X не является точкой оптимума функции . Однако, при соблюдении определенных условий, эта точка находится ближе к экстремальной точке, чем точка . Следовательно, на основании приближенного равенства можно сформировать рекуррентную процедуру:

,

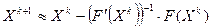где - градиент, а - матрица вторых производных функции f(X) в точке . Условием остановки итерационной процедуры является равенство нулю вектора , с учетом погрешности вычислений. Проведя сравнительный анализ уравнений, приходим к выводу, что они идентичны, если .

Метод отыскания экстремума функции f(X) с помощью данного соотношения носит название метода Ньютона-Рафсона. Формула находит применение не только для определения экстремума функции f (X), но и для отыскания корней системы нелинейных уравнений , i =1,2,…, n.

Методу Ньютона-Рафсона можно дать геометрическую интерпретацию на примере функции одной переменной. Пусть функция W (x) и ее производная имеют вид, как показано на рис. Из рисунка следует, что вторая производная функции W(x) - в точке равна отношению функции в точке к разности между точками и , . Отсюда, после элементарных преобразований, получим, 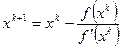. Но данное выражение есть не что иное, как одномерный аналог приведенной формулы. Таким образом, положение точки определяется пересечением касательной к функции в точке с осью абсцисс.

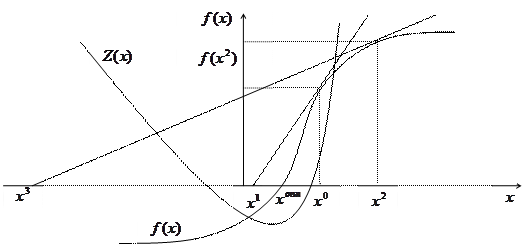
Рис. Графическая интерпретация метода Ньютона-Рафсона.

Сходимость метода зависит от выбора точки начального приближения. Покажем это. Из рисунка следует, что функция W(X) в точке имеет минимум, так как ее производная в этой точке равна 0, , а при переходе через точку производная меняет знак с минуса на плюс. Если в качестве точки начального приближения выбрать точку , то очередная точка - окажется ближе к точке . Следовательно, процесс сходится. Если же в качестве точки начального приближения взять точку , то точка , полученная в результате итерации, окажется дальше от точки , и процесс расходится.

Алгоритмы определения области сходимости функции W(X) достаточно сложны. На практике часто руководствуются следующим правилом. Если длина шага от итерации к итерации увеличивается, то процесс, скорее всего, расходится и необходимо выбирать иную точку начального приближения.

Поскольку равенство нулю градиента еще не гарантирует экстремума, для определения того, является ли найденная точка действительно экстремальной или только стационарной, нужны дополнительные меры. На практике для проверки точки на экстремальность часто прибегают к исследованию поведения функции W(X) в малой окрестности этой точки. Для этого вычисляют величину W(X) в некоторых, специальным образом подобранных, точках окрестности и сравнивают с величиной функции в самой точке, подозреваемой на экстремальность.

Известны различные модификации метода Ньютона-Рафсона: метод переменной метрики, метод сопряженных градиентов, и др. Эти методы отличаются более быстрой сходимостью, чем классический метод Ньютона-Рафсона, на определенных классах функций.

Пример 1. Найти максимум функции

.

Найдем градиент функции 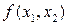и матрицу вторых производных. Получим: , где 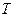– символ транспонирования, . Найдем матрицу обратную матрице вторых производных . Обратная матрица определяется по формуле , где: 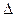- определитель матрицы , - алгебраические дополнения (i, j)-х элементов этой же матрицы. Таким образом, .

Только после этих предварительных расчетов можно приступать к итерационной процедуре отыскания максимума функции .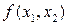

Шаг 1. В качестве точки начального приближения выберем точку 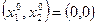. Подставив эту точку в формулу для вычисления градиента, получим, . Вычислим координаты точки первого приближения:

,

и градиент функции 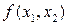в этой точке,

.

Так как градиент функции 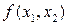в точке с координатами оказался равным 0, эта точка является стационарной и может содержать искомый максимум. В данном случае проверить стационарную точку на наличие в ней максимума легко. Для этого достаточно убедиться в том, что матрица вторых производных является отрицательно определенной (знак -го углового минора совпадает со знаком выражения .

Не нашли, что искали? Воспользуйтесь поиском: