
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Решение задач нелинейного программирования методом множителей Лагранжа
Метод множителей Лагранжа, как и метод приведенного градиента, предназначен для решения задач с дважды непрерывно дифференцируемыми целевыми функциями и функциями системы ограничений. Ограничения также задаются в виде равенств.
Выражение u = f (x, y) - lg(x, y) называется функцией Лагранжа.
Использование функции Лагранжа для нахождения точек экстремума функции называется также методом множителей Лагранжа.
Рассмотрим более сложную ситуацию, когда число переменных равно  .
.
Пусть дана оптимизационная задача
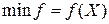 ,
,
 ,
,
где:  ,
,  , функция
, функция  и вектор-функция
и вектор-функция  непрерывны, имеют непрерывные 1 и 2 производные. Сформируем функцию Лагранжа
непрерывны, имеют непрерывные 1 и 2 производные. Сформируем функцию Лагранжа
 ,
,
где  - вектор множителей Лагранжа,
- вектор множителей Лагранжа,  . Для стационарной точки
. Для стационарной точки  функции Лагранжа имеют место условия:
функции Лагранжа имеют место условия:
 ,
,
 .
.
Можно показать, что необходимые условия существования экстремума для функции Лагранжа и для сформулированной оптимизационной задачи совпадают. Следовательно, задача условной оптимизации оказывается эквивалентной задаче безусловной оптимизации функции Лагранжа. Достаточные условия существования экстремума задачи в методе множителей Лагранжа определяются следующим образом.
 является точкой максимума оптимизационной задачи, если, начиная с главного минора порядка (m+1) матрицы H, следующие (n-m) главных миноров образуют знакопеременный числовой ряд, знак которого определяется множителем
является точкой максимума оптимизационной задачи, если, начиная с главного минора порядка (m+1) матрицы H, следующие (n-m) главных миноров образуют знакопеременный числовой ряд, знак которого определяется множителем  . Точка
. Точка  является точкой минимума, если, начиная с главного минора порядка (m+1) матрицы H, знаки последующих главных миноров определяются множителем
является точкой минимума, если, начиная с главного минора порядка (m+1) матрицы H, знаки последующих главных миноров определяются множителем 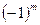 . Однако на практике, в силу большой вычислительной сложности, эти условия используются редко. Чаще наличие экстремума в стационарной точке проверяется с помощью исследования величины функции W(X) в малой окрестности этой стационарной точки.
. Однако на практике, в силу большой вычислительной сложности, эти условия используются редко. Чаще наличие экстремума в стационарной точке проверяется с помощью исследования величины функции W(X) в малой окрестности этой стационарной точки.
Пример. Решим методом множителей Лагранжа следующий пример. Найти минимум функции
 ,
,
при ограничениях:
 ,
,
 .
.
Запишем функцию Лагранжа:
 .
.
Возьмем производные функции Лагранжа по всем переменным. Получим систему уравнений:
 ,
, 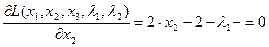 ,
,
 ,
,
 ,
,  .
.
Не нашли, что искали? Воспользуйтесь поиском: