
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Решение задач выпуклого программирования. Условия Куна-Таккера
Модель выпуклого программирования используется в том случае, если в рассматриваемой системе (объекте) целевая функция выпукла (вогнута) и область допустимых решений  , определяемая в общем случае нелинейными ограничениями, вогнута (выпукла).
, определяемая в общем случае нелинейными ограничениями, вогнута (выпукла).
С математической точки зрения общая модель выпуклого программирования описывается следующим образом.
Найти неотрицательные значения переменных  , удовлетворяющих ограничениям
, удовлетворяющих ограничениям  и доставляющих максимум (минимум) вогнутой (выпуклой) целевой функции
и доставляющих максимум (минимум) вогнутой (выпуклой) целевой функции  .
.
Для модели выпуклого программирования справедлива локально-глобальная теорема, в соответствии с которой локальный оптимум является и глобальным.
Для таких задач существуют условия оптимальности, определяемые теоремами (условиями) Куна-Таккера. Данные условия являются обобщением метода множителей Лагранжа при ограничениях-неравенствах,  .
.
Рассмотрим выпуклую задачу нелинейного программирования в случае ограничений-равенств. Функция Лагранжа будет иметь вид:

В случае ограничений неравенств необходимо максимизировать f (X) при ограничениях g (X) £ 0,  . Ограничения-неравенства можно преобразовать в равенства с помощью неотрицательных дополнительных переменных. Пусть Si 2 (Si 2³ 0) – дополнительная переменная, которая прибавляется к левой части i -го ограничения gi (X) £ 0. S =(S1, S2, …, Sm)T и S 2=(S12, S22, …, Sm2)T, где т – общее количество ограничений-неравенств.
. Ограничения-неравенства можно преобразовать в равенства с помощью неотрицательных дополнительных переменных. Пусть Si 2 (Si 2³ 0) – дополнительная переменная, которая прибавляется к левой части i -го ограничения gi (X) £ 0. S =(S1, S2, …, Sm)T и S 2=(S12, S22, …, Sm2)T, где т – общее количество ограничений-неравенств.
Задача оптимизации принимает вид:
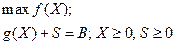
Следовательно, функция Лагранжа записывается в виде

Первая теорема. Для задачи выпуклого программирования множество допустимых решений обладает свойством регулярности:  является оптимальным тогда и только тогда, когда
является оптимальным тогда и только тогда, когда  является седловой точкой функции Лагранжа.
является седловой точкой функции Лагранжа.
Необходимые условия Куна – Таккера позволяют определять стационарные точки в задаче нелинейного программирования с ограничениями в виде неравенств при решении задач выпуклого программирования. В основу их получения положен метод множителей Лагранжа. Эти условия являются также и достаточными, если выполняются определенные правила, которые будут рассмотрены ниже.
Необходимым условием экстремума является равенство нулю всех частных производных. Но т.к. ограничения имеют вид равенств, то получим  . Поэтому исследование функции Лагранжа можно заменить исследованием целевой функции.
. Поэтому исследование функции Лагранжа можно заменить исследованием целевой функции.
При ограничениях g(X)£0 необходимым условием оптимальности в задаче максимизации (минимизации) является неотрицательность (соответственно, не положительность) множителей l.
Приведем обоснование этого. Рассмотрим задачу максимизации. Так как множители lвыражают скорость изменения целевой функции f (X) по отношению к изменениям g, т.е. l=  , то, как только правая часть ограничения g (X) £ 0 увеличивается и становится больше нуля, область допустимых решений задачи расширяется и, следовательно, оптимальное значение целевой функции f (X) не может уменьшиться. Это значит, что l ³ 0. Аналогично в случае задачи минимизации при увеличении правой части ограничения оптимальное значение функции f (X) не может увеличиться, откуда следует, что l£ 0. Если же ограничения задачи имеют вид равенств, т.е. g (X) =0, то компоненты вектора l по знаку не ограничены.
, то, как только правая часть ограничения g (X) £ 0 увеличивается и становится больше нуля, область допустимых решений задачи расширяется и, следовательно, оптимальное значение целевой функции f (X) не может уменьшиться. Это значит, что l ³ 0. Аналогично в случае задачи минимизации при увеличении правой части ограничения оптимальное значение функции f (X) не может увеличиться, откуда следует, что l£ 0. Если же ограничения задачи имеют вид равенств, т.е. g (X) =0, то компоненты вектора l по знаку не ограничены.
Условия Куна-Таккера для выпуклого программирования показывают, что оптимальный план находится в седловой точке функции Лагранжа. В седловой точке функция является выпуклой по одной переменной и вогнутой по другой.
 |  | ||
|

Для f (x) седловая точка – это такая точка x* =(x1*, x2*) в которой целевая функция f (x1, x2) принимает наименьшее значение по одной координате x1 и наибольшее значение по другой координате x2. В окрестности седловой точки для любых значений x1, x2 всегда выполняется: f (x1*, x2) £ f (x1*, x2*) £ f (x1, x2*).
Седловая точка может быть или внутри области допустимых значений или на границе. Пусть имеются две переменные  , то если она находиться внутри области, то в ее окрестности выполняется условие
, то если она находиться внутри области, то в ее окрестности выполняется условие
 .
.
Таким образом, в зависимости от типа седловой точки (на границе или внутри области допустимых значений) хотя бы один из сомножителей должен быть равен нулю.
Для выпуклой задачи нелинейного программирования условия Куна-Таккера в седловой точке для решения задачи максимизации имеют вид:

Условия Куна-Таккера являются необходимыми, но не достаточными для столь широкого класса задач условной оптимизации. Достаточными они являются для выпуклых (вогнутых) целевых функций и выпуклых областей допустимых решений. Если к тому же учесть, что задачи оптимизации достаточно часто имеют выгнутые (вогнутые) целевые функции и выпуклую область допустимых решений, становится понятным, почему в теории нелинейной оптимизации столь много внимания уделяется выпуклым функциям и выпуклым областям допустимых решений.
Функция является выпуклой, если все главные миноры матрицы вторых производных неотрицательны. Функция называется строго выпуклой, если все главные миноры положительные.
Достаточность условий Куна – Таккера. Если целевая функция и область допустимых решений рассматриваемой задачи обладают определенными свойствами, связанными с выпуклостью и вогнутостью, то необходимые условия Куна – Таккера являются также достаточными. Упомянутые свойства перечислены в таблице.
| Тип оптимизации | Требуемые свойства | |
| Целевая функция | Область допустимых решений | |
| Максимизация | Вогнутая | Выпуклое множество |
| Минимизация | Выпуклая | Вогнутое множество |
Процедура проверки выпуклости или вогнутости некоторой функции является более простой, чем доказательство выпуклости множества допустимых решений «задачи поиска экстремума». Так как выпуклость допустимого множества может быть установлена путем непосредственной проверки выпуклости или вогнутости функций ограничений,по этой причине приведем перечень требований, которые легче использовать на практике. Чтобы установить эти требования, рассмотрим задачу нелинейного программирования в общей постановке.
Максимизировать или минимизировать f (X) при ограничениях
g i (X) £ 0, i= 1, 2, …, r,
g i (X) ³ 0, i= r +1, …, р,
g i (X) = 0, i= р + 1, …, m.
Не нашли, что искали? Воспользуйтесь поиском: