Порядок выполнения работы. 1. Найдем графически отрезок [ небольшой длины h, изоли­рующий один из корней, и проверим результат аналитически.

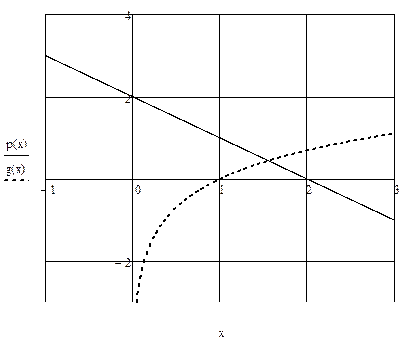1. Найдем графически отрезок [ 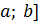небольшой длины h, изоли­рующий один из корней, и проверим результат аналитически.

ОДЗ: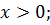

Графически:

Из графика:

Аналитически:

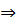функция возрастает при 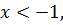убывает при 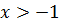. Учтем ОДЗ 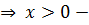функция монотонно возрастает.

Найдем 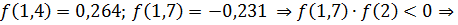на отрезке существует один корень

2. Приведем исходное уравнение к виду 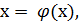пригодному для метода простой итерации на отрезке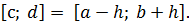

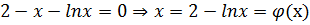
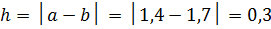
Тогда отрезок

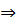итерационный процесс сходится при любом

3. Вычислим вручную 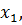определим его абсолютную погреш­ность и проверим условие окончания итерационного процесса.

За возьмем Тогда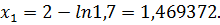

.

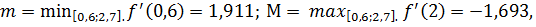
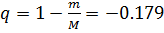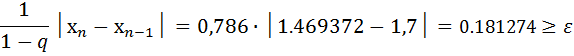
4. Напишем программу вычисления приближений до достиже­ния требуемой точности ε с выводом в таблицу номера итерации, значения на этом этапе, и абсолютной погрешности на данном этапе приближения.

Примечание: через 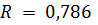обозначен коэффициент .

Текст программы:

var

i:integer;

x,x0,r,e:real;

function f(x:real):real;

begin

f:=2-ln(x);

end;

begin

write('x0='); readln(x);

write('e='); readln(e);

r:=0.786;

i:=0;

repeat

x0:=x;

x:=f(x0);

i:=i+1;

writeln('iteraciya#',i,' x=',x:1:6,

' pogrewnost=',(R*abs(x-x0)):1:6);

until r*abs(x-x0)<=e;

writeln('x=',x:1:6);

readln

end.

Результат, выведенный на экран:

x0=1.7

eps=0.000005

iteraciya#1 x=1.469372 pogrewnost=0.181274

iteraciya#2 x=1.615165 pogrewnost=0.114594

iteraciya#3 x=1.520563 pogrewnost=0.074357

iteraciya#4 x=1.580919 pogrewnost=0.047440

iteraciya#5 x=1.541993 pogrewnost=0.030596

iteraciya#6 x=1.566924 pogrewnost=0.019595

iteraciya#7 x=1.550886 pogrewnost=0.012606

iteraciya#8 x=1.561174 pogrewnost=0.008087

iteraciya#9 x=1.554562 pogrewnost=0.005197

iteraciya#10 x=1.558806 pogrewnost=0.003336

iteraciya#11 x=1.556080 pogrewnost=0.002143

iteraciya#12 x=1.557830 pogrewnost=0.001376

iteraciya#13 x=1.556706 pogrewnost=0.000884

iteraciya#14 x=1.557428 pogrewnost=0.000568

iteraciya#15 x=1.556964 pogrewnost=0.000364

iteraciya#16 x=1.557262 pogrewnost=0.000234

iteraciya#17 x=1.557071 pogrewnost=0.000150

iteraciya#18 x=1.557194 pogrewnost=0.000097

iteraciya#19 x=1.557115 pogrewnost=0.000062

iteraciya#20 x=1.557165 pogrewnost=0.000040

iteraciya#21 x=1.557133 pogrewnost=0.000026

iteraciya#22 x=1.557154 pogrewnost=0.000016

iteraciya#23 x=1.557140 pogrewnost=0.000011

iteraciya#24 x=1.557149 pogrewnost=0.000007

iteraciya#25 x=1.557143 pogrewnost=0.000004

otvet: x=1.557143

5. Найдите приближенный корень и выпишите его с верными зна­чащими цифрами.

Ответ: у уравнения один корень на , который был вычислен с точностью ε = 0,5 10^-5:

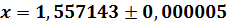, либо

Не нашли, что искали? Воспользуйтесь поиском: