
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Методы отделения корней уравнений
Чем меньше длина отрезка изоляции, тем выше точность приближения, однако с помощью используемых для отделения корней приемов получить отрезок достаточно малой длины трудно. Нужны специальные методы уточнения корней. Далее в главе будет рассмотрено несколько таких методов, которые реализуют следующие два способа поиска приближенного корня с заданной точностью ε > 0:
1. Последовательно уменьшая длины отрезка изоляции корня по какому-либо правилу, отыскивается отрезок  такой, что
такой, что  и
и  . Тогда приближенным корнем требуемой точности будет середина отрезка
. Тогда приближенным корнем требуемой точности будет середина отрезка 
2. Строится последовательность чисел  сходящаяся к корню t. Как только окажется
сходящаяся к корню t. Как только окажется  , можно положить
, можно положить  Такая последовательность называется последовательностью приближений, а определяющий ее метод — методом последовательных приближений.
Такая последовательность называется последовательностью приближений, а определяющий ее метод — методом последовательных приближений.
Первый способ удобен тем, что позволяет легко устанавливать завершение процесса уточнения, поскольку отрезки изоляции и их длины на каждом шаге вычислений известны.
Непосредственную проверку условия  из второго способа проводить не удается, ибо неизвестен точный корень t. В то же время для каждого метода последовательных приближений есть возможность получить неравенства вида
из второго способа проводить не удается, ибо неизвестен точный корень t. В то же время для каждого метода последовательных приближений есть возможность получить неравенства вида

Здесь Vn — числовое выражение, значения которого при каждом η характеризуют степень близости приближения  к корню, обеспечиваемую данным методом. За условие окончания процесса приближений можно взять неравенство:
к корню, обеспечиваемую данным методом. За условие окончания процесса приближений можно взять неравенство:  .
.
Абсолютной погрешность каждого приближения  ибо ясно, что
ибо ясно, что 
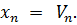
4.2. Алгоритм построения итерационной последовательности, порождаемой уравнением 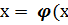 )
)
Рассмотрим уравнение вида х=g(х) с корнем t, отделенным на отрезке 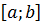 . Функция g предполагается непрерывной на этом отрезке. Уравнение х=g(х) можно получить из уравнения f(x) = 0 путем эквивалентных преобразований. Метод простой итерации является одним из наиболее удобных и эффективных методов приближенного решения уравнений, он предполагает уточнение корня с использованием итерационной последовательности.
. Функция g предполагается непрерывной на этом отрезке. Уравнение х=g(х) можно получить из уравнения f(x) = 0 путем эквивалентных преобразований. Метод простой итерации является одним из наиболее удобных и эффективных методов приближенного решения уравнений, он предполагает уточнение корня с использованием итерационной последовательности.
Рекуррентная формула определяется на основе самого уравнения х=g(х). Если известен какой-либо член последовательности  (например,
(например,  ), то за
), то за  , можно взять
, можно взять  . Соотношение
. Соотношение  является искомой рекуррентной формулой.
является искомой рекуррентной формулой.
4.3. Достаточное условие сходимости итерационной последовательности
Пусть корень t уравнения х=g(х) отделен на отрезке  длины h. Если на отрезке
длины h. Если на отрезке  функция g дифференцируема и найдется число
функция g дифференцируема и найдется число  такое, что
такое, что  при всех
при всех  , то итерационная последовательность, порожденная формулой х=g(х), сходится к корню t при любом выборе начального приближения
, то итерационная последовательность, порожденная формулой х=g(х), сходится к корню t при любом выборе начального приближения 
Не нашли, что искали? Воспользуйтесь поиском: