Алгоритм метода половинного деления

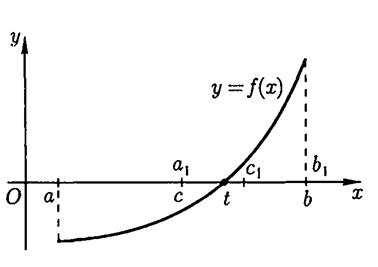Пусть f непрерывна на и 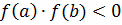. Разделим пополам точкой и вычислим f (с). Если f (с) = 0, то корень t найден точно (а именно, ). Если же нет, выберем ту половину отрезка, на концах которой значения фун­кции разных знаков, и обозначим ее [ а₁; b₁ ] (на рис. 3 правая поло­вина ). Затем отрезок [ а₁; b₁ ] делим пополам точкой 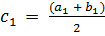и проводим аналогичные рассуждения. Получится либо точный ко­рень с₁, либо отрезок [а₂; b₂]со свойством .

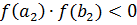И так далее, пока функция от с_n не будет равна нулю (или пока не будет выполняться условие окончания процесса при заданной погрешности).

2.5. Условие окончания процесса деления при заданной допусти­мой погрешности

Для того чтобы найти приближенное значение корня с точнос­тью до ε > 0, необходимо остановить процесс половинного деления па таком шаге n, на котором отрезок [ а_n; b _n], будет иметь длину

и вычислить 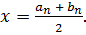Тогда можно взять 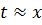, причем .

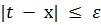Задание

Отделите корни данного уравнения и уточните их методом поло­винного деления с точностью до ε = 0,5 10^-4.

Вариант	Уравнение

1. Отделим графически все корни уравнения f(x) = 0 так, чтобы на отрезках изоляции корней функция f удовлетворяла условиям метода половинного деления.

Из графика примем

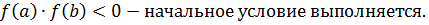
2. Выполним один шаг метода для одного из корней вручную и проверим условие окончания вычислений.

3. Составим программу уточнения корня с точностью до ε, выводящую в таблицу номер итерации, концы вложенных отрезков и их длины.

Текст программы:

var

x,y,x0,x1: real;

e,a,dlina,b: real;

l,n,i:integer;

function f(x: real):real;

begin

f:=(sin(x-0.5))-2*x+0.5;

end;

begin

a:=-0.3;

b:=0.5;

write('e=');

readln(e);

x0:=a;

x1:=b;

while true do

begin

x:=(x0+x1)/2;

y:=f(x);

l:=1;

n:=n+1;

dlina:=(x1-x0)/l;

if dlina<e then

begin

writeln('x=',x:1:6);

break

end

else

begin

for i:=1 to n do l:=l*2;

if y*f(x0)>0 then x0:=x

else x1:=x;

writeln ('[',x0:1:6,';',x1:1:6,'] ',

'iteracia #', n,

' ',

'dlina otrezka',

' ',

dlina:1:4);

end

end;

readln

end.

Результат, выведенный на экран:

e=0.00005

[-0.300000;0.100000] iteracia #1 dlina otrezka 0.8000

[-0.100000;0.100000] iteracia #2 dlina otrezka 0.4000

[-0.000000;0.100000] iteracia #3 dlina otrezka 0.2000

[-0.000000;0.050000] iteracia #4 dlina otrezka 0.1000

[-0.000000;0.025000] iteracia #5 dlina otrezka 0.0500

[0.012500;0.025000] iteracia #6 dlina otrezka 0.0250

[0.012500;0.018750] iteracia #7 dlina otrezka 0.0125

[0.015625;0.018750] iteracia #8 dlina otrezka 0.0063

[0.017187;0.018750] iteracia #9 dlina otrezka 0.0031

[0.017969;0.018750] iteracia #10 dlina otrezka 0.0016

[0.018359;0.018750] iteracia #11 dlina otrezka 0.0008

[0.018359;0.018555] iteracia #12 dlina otrezka 0.0004

[0.018359;0.018457] iteracia #13 dlina otrezka 0.0002

[0.018359;0.018408] iteracia #14 dlina otrezka 0.0001

x=0.018384

4. Найдите все приближенные корни уравнения и выпишите их с верными значащими цифрами.

Ответ: у уравнения sin(x - 0,5)– 2x+0,5 = 0 один корень на , который был вычислен с точностью ε = 0,5 10^-4:

;

Не нашли, что искали? Воспользуйтесь поиском: