Алгоритм уточнения корней комбинированным методом хорд н касательных

1. Вычислить значения f(a) и f(b);

2. Проверить выполнение условия 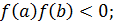если условие не выполняется, неверно выбран отрезок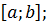

3. Найти первую и вторую производные f;

4. Проверить постоянство знака производных на отрезке 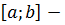если условие не выполняется, он выбран неверно;

5. Выполнить действия, указанные в п.3.3.;

6. Проверить условие окончания процесса, если задана погрешность; если оно не выполняется, то отрезок изоляции корня сужается и имеет вид . Приближенные корни находят по формулам

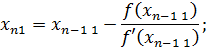
3.5. Условие окончания процесса вычислений при заданной допус­тимой погрешности

Для того чтобы найти приближенное значение корня с точнос­тью до ε > 0, необходимо остановить процесс половинного деления па таком шаге n, на котором отрезок [ x_n1 ; x _n2], будет иметь длину

и вычислить Тогда можно взять , причем .

Проверяется условие , где ε – заданная точность. Вычисления продолжаются до тех пор, пока не будет найдено такое значение , при котором и 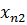не совпадут с точностью ε.

Задание

Отделите аналитически один из корней данного уравнения и оп­ределите его с точностью до ε = 0,5 · 10^-5 комбинированным мето­дом хорд и касательных.

Вариант	Уравнение

1. Отделим корни уравнения аналитически и выберем один из отрезков изоляции, на котором выполняются условия применимо­сти метода.

Нули 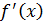: Тогда при функция возрастает, а при – убывает. Примем за

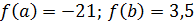. Так как 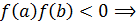на отрезке существует один корень.

отрезок выбран верно.

2. Возьмем соответствующие начальные приближения и найдем вручную первые приближения. Проверим условие окончания процесса вычислений.

Проверим условие :

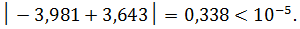
3. Составим программу уточнения корня с точностью до ε, кото­рая выводила бы приближения к корню, найденные методами хорд и касательных, и расстояния между ними, в таблицу.

Текст программы:

function f(var x:real):real;

begin

f:= 2*X*X*X+9*X*X-21;

end;

function f1(var x:real):real;

begin

f1:= 6*X*X+18*X;

end;

function f2(var x:real):real;

begin

f2:= 12*X+18;

end;

var

a,b,e,e1,x0,x11,x12:real;

n:integer;

begin

a:=-4.5;

b:=-3.5;

e:=0.000005;

x0:=a;

n:=1;

if f(a)*f(b)>0 then writeln('otrezok vibran neverno')

else

begin

x11:=x0-f(x0)/f1(x0);

x12:=a-((b-a)*f(a)/(f(b)-f(a)));

e1:=(x11+x12)/2;

writeln ('x11=',x11:1:6,' x12=',x12:1:6,' iteraciya #',n, ' x=',e1:1:6);

while abs(x11-x12)>=2*e do

begin

a:=x11;

b:=x12;

x11:= a-F(a)/f1(a);

x12:= a-((b-a)*f(a)/(f(b)-f(a)));

e1:=(x11+x12)/2;

n:=n+1;

writeln ('x11=',x11:1:6,' x12=',x12:1:6,' iteraciya #',n, ' x=',e1:1:6)

end;

writeln ('x=',e1:1:6)

end;

readln

end.

Результат, выведенный на экран:

x11=-3.981481 x12=-3.642857 iteraciya #1 x=-3.812169

x11=-3.786967 x12=-3.736732 iteraciya #2 x=-3.761849

x11=-3.756286 x12=-3.755065 iteraciya #3 x=-3.755676

x11=-3.755532 x12=-3.755531 iteraciya #4 x=-3.755531

x=-3.755531

4. Найдите приближенный корень и выпишите его с верными зна­чащими цифрами.

Ответ: на отрезке существует только один корень данного уравнения, который был вычислен с точностью до ε = 0,5 · 10^-5:

.