Екстремуми функцій багатьох змінних. Умовний екстремум.

Нехай функція z=f(x;y) визначена в деякій області точки (х₀,у₀). Кажуть, що функція z=f(x;y) має в точці (х₀,у₀) строгий максимум (мінімум), якщо f(x;y)<f(x₀;y₀) (f(x;y)>f(x₀;y₀)) для всіх точок (х;у), достатньо близьких до х₀, у_{0 .} Точка (х₀,у₀) – точка максимуму (мінімуму).

Максимум і мінімум функції називають екстремумами функціями.

Теорема 1 (необхідні умови екстремуму).

Якщо диференційована функція z=f(x;y) має екстремум в точці Р₀ (х₀,у₀), то її частинні похідні першого порядку в цій точці дорівнюють нулю, тобто , .

Теорема 2 (достатні умови існування екстремуму).

Нехай функція z=f(x;y) неперервна в D(f) разом зі своїми частинними похідними першого і другого порядків і точка Р₀(х₀,у₀) є критичною.

Знайдемо в точці Р₀ похідні другого порядку і позначимо:

, , .

Якщо AC-B²>0, то функція має в точці Р₀(х₀,у₀) екстремум: максимум якщо А<0 і мінімум якщо А>0.

Якщо АС-B²<0, то в точці Р₀(х₀,у₀) екстремуму немає.

Якщо АС-В²=0, то висновок про екстремум зробити не можна.

Умовний екстремум

Нехай задано функцію , стосовно якої ставиться вимога знайти її екстремуми при умові, що - рівняння розв’язку.

Ця задача умовного екстремуму зводиться до знаходження звичайного екстремуму функції

.

Де F – функція Лагранжа; - множник Лагранжа.

Стаціонарні точки знаходять із системи рівнянь

Характер умовного екстремуму можна встановити за знаком диференціала другого порядку функції Лагранжа: якщо у стаціонарній точці , то це є точка умовного мінімуму (максимуму).

Приклад. (На умовний екстремум). Знайти екстремум функції при умові .

Функція Лагранжа буде мати вигляд

Запишемо необхідні умови існування екстремуму:

.

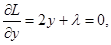
Звідки отримуємо:

та

Критична точка буде мати координати:

, .

,

,

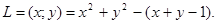
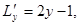
Тоді

Отже існує min функції

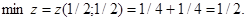
Не нашли, что искали? Воспользуйтесь поиском: