Первісна функція та невизначений інтеграл

Задачею диференціального числення було знаходження похідної від заданої функції y=f (x). Задача інтегрального числення протилежна: потрібно визначити функцію, похідна від якої відома.

Означення. Функція F (x) називається первісною для функції f (x), якщо f ¢(x)= F (x).

Приклад. Для функції y =3 x ² первісними є функції F (x)= x ³; F (x)= x ³+5; F (x)= x ³-6,3 тощо.

Означення. Невизначеним інтегралом від функції f (x) називається сукупність усіх первісних цієї функції.

Використовується позначення

,

де f (x) dx - підінтегральний вираз, а C - стала інтегрування.

З геометричного погляду невизначений інтеграл – це сукупність (сім’я) ліній F (x)+ C (рис. 7.1).
Наведемо таблицю основних інтегралів. Доведення кожної рівності полягає у її диференціюванні.

(n ¹-1), у тому числі

;

;

;

;

, у тому числі ;

;

;

;

;

, у тому числі ;

, у тому числі ;

.

Із означення невизначеного інтеграла випливають такі властивості інтегрування:

1) ;

2) ;

3) (метод заміни змінних, метод підстановки);

4) (інтегрування частинами).

Отже,

.

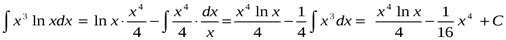Знайти . Позначимо u=x, dv = e ^2x dx. Звідси du=dx, v =(1/2)× e ^2x. Тоді

.

Для інтегрування раціональних дробів, тригонометричних виразів тощо, використовуєть спеціальні прийоми. Розглянемо два приклади відшукання невизначених інтегралів від раціональних дробів.
50))))

Означення. Нехай функція F — первісна для f на J. Невизначеним інтегралом від функції f називається сукупність усіх первісних цієї функції, тобто вираз

де C ∈ R — довільна стала.

Функція f називається підінтегральною функцією, f(x)dx — підінтегральним виразом, C — сталою інтегрування, x — змінною інтегрування.

З геометричної точки зору невизначений інтеграл — це сукупність (сім'я) ліній F(x) + C (див. Рис.).

Властивості невизначеного інтеграла

З означень первісної та невизначеного інтеграла випливають наступні властивості (за умов існування первісних та похідних на інтервалі J):

51)))Метод підстановки (заміни змінної)

Цей метод містить два прийоми.

a) Якщо для знаходження заданого інтеграла ∫f(x)dx зробити підстановку x = φ(t), тоді має місце рівність: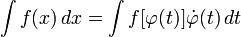

Після знаходження останнього інтеграла треба повернутись до початкової змінної інтегрування х. Для застосування цього прийому треба, щоб функція х - φ (t) мала обернену t = ψ(х).

Приклад. Знайти інтеграл

Розв'язування. Зробимо підстановку х = 5sint, тоді

Отже, одержимо

Із рівності х = 5sin t одержимо t = arcsin (х/5);

Отже,

b) Якщо зробити заміну змінної, тобто t = φ (х) тоді має місце рівність:

Після знаходження останнього інтеграла треба повернутись до змінної х, використовуючи рівність t = φ (х).

Приклад. Знайти

Розв’язування. Нехай тоді .

Не нашли, что искали? Воспользуйтесь поиском: