
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Асимптоты графика (горизонтальные, вертикальные, наклонные)
Асимптотой графика функции y=f(x) называется прямая, к которой график функции как угодно приближается, но не пересекает ее. 1. Если lim x→x0 f(x)=∞, x=x0 –вертикальная асимпт (lim x→x0 -0 f(x)=∞ или lim x→x0 +0 f(x)=∞) 2. Если lim x→∞ f(x)=b, то y=b- горизонтальная асимптота 3. Если y=kx+b-наклонная асимптота, то k=lim x→∞ f(x)/x, в lim x→∞ (f(x) – kx)
Вопрос№52
Общая схема исследования и построения графика функции
1. D(y), E(y);
2. Свойства (четность/нечетность, периодичность);
3. Асимптоты
4. Нули функции
5. Производная, экстремум
6. y”, ∩/U, точки перегиба
7. Пару контрольных точек
8. График
Вопрос№53
Дифференциал функции, его геометрический смысл. Свойства дифференциала.
Дифференциал функции y=f(x)-величина dy=f’(x)∆x dy=f(x)dx → f’(x)=dy/dx Геометрический смысл дифференциала Выясним геометрический смысл дифференциала. Для этого проведём к графику функции у = f (х) в точке М (х; у) касательную МТ и рассмотрим ординату этой касательной для точки х + Δх (рис.
Но, согласно геометрическому смыслу производной, tg α = f ′ (х). Поэтому АВ = f ′ (х)⋅Δх.
Сравнивая полученный результат с формулой получаем dy = АВ, т.е. дифференциал
функции у = f (х) в точке х равен приращению ординаты касательной к графику функции в этой
точке, когда х получит приращение Δх.
Дифференциал функции приближенно равен приращению функции ∆y и пропорционален приращению аргумента ∆x.
Свойства дифференциала:
1. d (c) = 0; d(c u) = c du;
2. d(u v) = d u d v;
3. d(u v) = v d u + u dv;
4. d(u / v) = (v d u - u d v) / v 2
Вопррос54
Инвариантность формы дифференциала. Применение дифференциала в приближенных вычислениях. Дифференциал n-ого порядка.
Инвариантность (неизменность) формы дифференциала. Этим свойством обладает дифференциал функции, но не обладает его производная.
1.Если y=f(x), dy=f’(x) dx
2.Если y=f(u), u=u(x), dy=f’(u)du
Применение дифференциала в приближенных вычислениях.
∆y≈dy=f’(x)∆x; ∆y=f(x+∆x)-f(x)
Заменим приращение разностью функций и получим:f(x0+  -f(x)
-f(x) 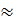 f ‘(x0)
f ‘(x0)  или f(x0+
или f(x0+  )
) 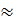 f(x)+f’(x0)
f(x)+f’(x0) 
Дифференциал n-ого порядка.
Дифференциалом n -го порядка называют дифференциал от дифференциала n-1 -го порядка.
Иначе дифференциал n-го порядка можно записать следующим образом dny=f n (x)dxn. В том случае, когда y=f(x), x=g(t), получаем dy= 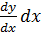 (по свойству инвариантности дифференциала).
(по свойству инвариантности дифференциала).
Тогда d2y=d(dy)=d(f ’ (x)dx)=d(f ’ (x))dx+f’(x)d(dx))=f ” (x)dx2+f ‘ (x)d2x.
Дифференциалы более высоких порядков не обладают свойством инвариантности в отличие от дифференциалов 1-ого порядка
Не нашли, что искали? Воспользуйтесь поиском: