Дифференциальное уравнение называется однородным уравнением 1-го порядка.

Его решение можно найти с помощью введения новой неизвестной функции по формуле . В случае такой замены имеют место очевидные соотношения .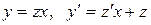

Пример. Найти общее решение уравнения

.

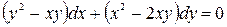Решение. Разделив обе части уравнения 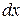на и на 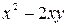, приведем его к виду

или .

Правая часть уравнения зависит только от отношения , то есть это однородное уравнение 1-го порядка. Полагаем , получим уравнение

.

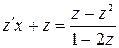Произведем в нем разделение переменных:

,

,

.

(обе части уравнения делим на , считая здесь, что ).

Тогда, , откуда, заменяя , найдем , или . Подставив и упростив, получим .

Если же , то , и, значит, и 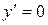. Подставив в первоначальное уравнение, получим . Значит, тоже является решением данного уравнения.

Ответ. .

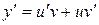3. Уравнение вида называется линейным дифференциальным уравнением 1-го порядка. Его решение можно найти в виде произведения двух функций, то есть полагая . Тогда . Подставляя в уравнение, получим

.

Найдем функцию , удовлетворяющую уравнению . Тогда для функции получим уравнение . Если – его общее решение, то общее решение данного линейного уравнения имеет вид .

Пример. Найти общее решение уравнения .

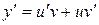Решение. Перепишем уравнение в виде . Это линейное дифференциальное уравнение 1-го порядка. Ищем решение в виде , тогда . Подставляя в уравнение, получим

.

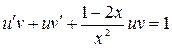Для получим уравнение . Разделяем в нем переменные и интегрируем:

.

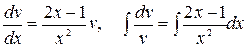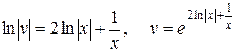, или .

Тогда для функции получим уравнение

,

откуда 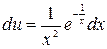. Интегрируем обе части этого равенства:

.

Тогда .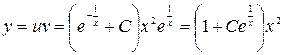

Ответ: .

К задачам 291 − 300.

Для решения этих уравнений нужно знать методы понижения порядка дифференциального уравнения.

1. Если дифференциальное уравнение 2-го порядка не содержит явно функцию , т.е. имеет вид , то полагаем , где – функция от . Тогда , и получаем дифференциальное уравнение 1-го порядка относительно новой неизвестной функции .

Пример. Уравнение не содержит функцию . Обозначим , тогда . Подставляя в данное уравнение, получим . В этом уравнении можно разделить переменные:

,

.

Интегрируя, получим , откуда . Подставив , получим 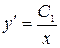, тогда 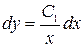и .

2. Если дифференциальное уравнение не содержит явно аргумент , т.е. имеет вид , то полагаем , где – функция от .

Тогда 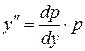. Получаем дифференциальное уравнение 1-го порядка относительно новой неизвестной функции .

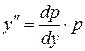Пример. В дифференциальном уравнении отсутствует . Обозначим , где , тогда . Получаем уравнение , или .

Если , то 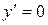, то есть . При 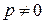получим уравнение 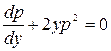. В нем можно разделить переменные и проинтегрировать:

,

,

откуда . Подставив здесь , получим . Это тоже дифференциальное уравнение с разделяющимися переменными:

, ,

откуда, интегрируя, найдем соотношение .

Ответ: .

К задачам 301 − 310.

1. Общее решение линейного неоднородного дифференциального уравнения 2-го порядка

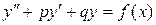(1)

равно сумме общего решения соответствующего однородного уравнения

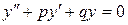
и какого-нибудь частного решения неоднородного уравнения (1), то есть .

2. Если – числа, то для нахождения нужно определить корни характеристического уравнения

. (2)

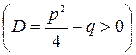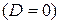Если действительные не равные друг другу корни , то ; если , то ; если корни комплексные, , то .

3. Пусть правая часть данного неоднородного уравнения (1) имеет вид

,

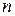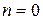
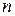где – многочлен степени . Отметим, что при – константа, а если , то – многочлен степени . Тогда частное решение можно найти в виде

,

где – некоторые коэффициенты, , если число не является корнем характеристического уравнения (2) (и тогда ), , если один из корней уравнения (2) равен , другой не равен , , 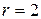если оба корня уравнения (2) равны .

Для случая, когда частное решение можно найти в виде

,

где – некоторые коэффициенты;

, если не является корнем характеристического уравнения (2) (и тогда ),

, если является корнем уравнения (2).

Коэффициенты () находят, подставляя функцию и ее производные в уравнение (1) и приравнивая коэффициенты при одинаковых функциях в обеих частях полученного равенства.

4. Если в правой части уравнения (1) стоит сумма функций различного вида , то частное решение равно сумме частных решений , где – решение уравнения (принцип наложения частных решений).

5. Константы находят из начальных условий , .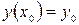

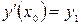Пример. Найти частное решение уравнения , удовлетворяющее начальным условиям .

Решение. Запишем характеристическое уравнение , откуда , . Общее решение соответствующего однородного уравнения имеет вид .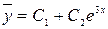

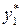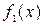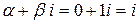В правой части нашего уравнения стоит сумма двух функций и . Частное решение , соответствующее правой части , нужно искать в виде , т.к. – многочлен степени поскольку число 0 является корнем характеристического уравнения. Частное решение , соответствующее правой части , ищем в виде (в данном случае , это число не является корнем характеристического уравнения). По принципу наложения частных решений . Находим производные:

,

.

Подставив в данное уравнение, получим

.

Приравниваем коэффициенты при одинаковых функциях. При , при , при , при 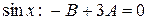. Из этой системы уравнений найдем, что , , , 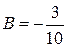. Подставив эти числа в и сложив и , найдем общее решение данного уравнения:

.

Для нахождения частного решения, удовлетворяющего начальным условиям , дифференцируем :

.

Подставляем 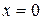в и в , получаем:

откуда 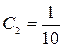и . Значит, – искомое частное решение.

К задачам 311 − 320.

Для решения линейной неоднородной системы дифференциальных уравнений

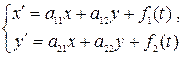
можно использовать метод исключения неизвестной функции. Если a ₁₂¹0, то из первого уравнения можно выразить неизвестную функцию y и подставить во второе уравнение, или наоборот, если a ₂₁¹0, то из второго уравнения выразить неизвестную функцию x и подставить в первое. Получим линейное дифференциальное уравнение второго порядка, решив которое, найдём одну неизвестную функцию. Другую неизвестную функцию находим с помощью формулы, использованной при исключении. Неизвестные функции будут зависеть от двух произвольных постоянных, которые находим из начальных условий.

Пример. Решить задачу Коши:

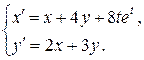x (0) = − 1, y (0) = 1.

Решение. Из второго уравнения системы выразим x:

(1)

и подставим в первое уравнение, исключив неизвестную функцию x.

,

,

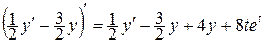. (2)

Получили линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами относительно неизвестной функции y. Найдём общее решение этого уравнения.

Запишем характеристическое уравнение: k ² – 4 k – 5 = 0. Его корни k ₁=5, k ₂= − 1. Общее решение соответствующего однородного дифференциального уравнения .

Правая часть дифференциального уравнения (2) имеет вид ,где a = 1, n = 1, т.е. 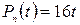– многочлен первой степени. Значит, частное решение дифференциального уравнения (2) нужно искать в виде , где r = 0, т.к. число a = 1 не является корнем характеристического уравнения (см. указания к задачам 301 – 310). Найдём неопределённые коэффициенты А и В.

,

,

.

Подставляя в дифференциальное уравнение (2) и приравнивая коэффициенты при линейно независимых функциях, получим:

;

;

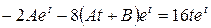Таким образом, − частное решение дифференциального уравнения (2), а − общее решение этого дифференциального уравнения.

Вторую неизвестную функцию находим по формуле (1).

Запишем общее решение данной системы дифференциальных уравнений:

Из начальных условий находим постоянные c₁ и c₂.

Ответ. .

К задачам 321− 330.

1. При составлении дифференциального уравнения в задачах с физическим содержанием нужно помнить следующее:

1) скорость изменения некоторой физической величины – это производная по времени , а ускорение – вторая производная ;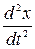

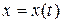2) прямолинейное движение материальной точки массы подчи-няется второму закону Ньютона , где – координата точки в момент времени , – сила, действующая на точку.

2. При составлении дифференциального уравнения кривой используется геометрический смысл производной ( дает нам угловой коэффициент касательной к кривой) или уравнение касательной, проведенной в некоторой точке : , где – координаты точки на касательной.

Пример. Найти уравнение кривой, проходящей через точку (1;0) и обладающей тем свойством, что ордината точки пересечения касательной с осью равна длине радиус-вектора точки касания.

Решение. Пусть искомая линия имеет уравнение , и пусть касательная проведена в некоторой точке этой кривой. Тогда длина радиус-вектора будет равна 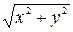. Положим 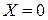в уравнении касательной , тогда – ордината точки пересечения касательной с осью . Из условия задачи получаем уравнение .

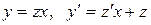Перепишем уравнение в виде . Это однородное уравнение 1-го порядка. Положим , тогда . Получим дифференциальное уравнение , или . Разделяем переменные и интегрируем:

.

Подставим :

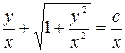или .

Подставив 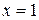и , получим и искомое уравнение 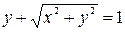. Его можно преобразовать:

.

Ответ: .

Не нашли, что искали? Воспользуйтесь поиском: