Дифференциалы высших порядков

Пусть функция z=f(x,y) имеет непрерывные первые и вторые частные производные на некотором плоском открытом множестве G. Из непрерывности частных производных следует дифференцируемость самой функции f(x,y) в каждой точке этого множества. Таким образом для всех точек (x,y) определен дифференциал:

Т.к. существуют непрерывные вторые производные, то функции и также дифференцируемые на этом множестве G. Поэтому дифференциал dz, рассматриваемый как функция только переменных x и y, в свою очередь является дифференцируемой функцией на множестве G.

Вычислим дифференциал от первого дифференциала, считая dx и dy фиксированными, т.е. dx и dy не меняются при переходе от одного дифференциала к следующему. Тогда:

d(dx)=0 и d(dy)=0, так как dx и dy фиксированные точки.

(*)

Опр.2: Вторым дифференциалом d²z функции z=f(x,y) в данной точке называется квадратичная форма от дифференциалов dx и dy независимых переменных (*).

Аналогично для функции n переменных y=f(x₁, x₂,…, x_n) второй дифференциал определяется по формуле:

- квадратичная форма относительно переменных х₁, х₂,…, х_n

Вообще дифференциал порядка l от функции y=f(x₁, x₂,…, x_n) определяется с помощью рекуррентной формулы:

Для функции z=f(x,y) при непрерывных частных производных 3-его порядка можно записать третий дифференциал:

Можно показать, что для дифференциала порядка m справедлива формула:

где

Формула Тейлора

Пусть z=f(x,y) имеет в окрестности точки Р₀(х₀,у₀) непрерывные производные всех порядков до порядка m. Р₁(х₀+Dх,у₀+Dу) соединим с Р₀ отрезком прямой, уравнение которой можно записать в параметрической форме:

х=х₀+tDх y=y₀+tDy t'[0,1] Dx=x-x₀ Dy=y-y₀

Тогда вдоль отрезка Р₀Р₁ функция z=f(x,y) будет функцией одной переменной:

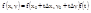(1)

Формула Маклорена для функции F(t) в окрестности точки t₀=0 имеет вид:

Полагая в этой формуле t=1получим:

Вычислим производную F(t) через функцию f(x,y).

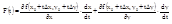
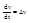
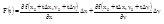
t=0

Аналогично:

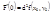
Аналогично:

В силу этого:

Последняя формула называется формулой Тейлора с остаточным членом формулы Лагранжа для функции f(x,y).

Для случая n переменных формула Тейлора имеет следующий вид:

Не нашли, что искали? Воспользуйтесь поиском: