Производная по направлению. Градиент.

Пусть функция f определена в d окрестности точки М₀ U(M₀,d) и пусть точка М₁' U(M₀,d). Проведем через точки М₀ и М₁ прямую. За положительное направление на этой прямой возьмем направление вектора 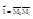. Для любых М М₀М – ориентированная длина, т.е. длина отрезка со знаком плюс, если вектор имеет то же направление, что и , и со знаком минус в противном случае.

Опр.1: 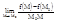, если он существует, называется производной функции f в точке х₀ по направлению и обозначается

Пусть в R³ зафиксирована некоторая система координат xyz M₀(x₀, y₀, z₀), M(x, y, z)

Dx=x-x₀ Dy=y-y₀ Dz=z-z₀

M₀K=x-x₀= M₀Mcosa

MK=y-y₀=M₀Mcosa

S=М₀М

Найдем связь между координатами точки М и ориентированной длиной S отрезка [М₀М]. Пусть a, b, g - это углы, образованные соответственно с осями Ох, Оу, Оz. Тогда:

х-х₀=S×cosa

y-y₀=S×cosb

z-z₀=S×cosg

вдоль прямой М₀М функция z=f(x,y,z) является функцией одной переменной S:

f(x,y,z)=f(x₀+Scosa, y₀+Scosb, z₀+Scosg)

Производная этой функции, если она существует, по переменной S является производной функции f в точке М₀ по направлению М₀М₁.

Вычисляется производная по направлению по правилу дифференцирования сложных функций.

Пусть функция f(x,y,z) дифференцируема в точке (x₀, y₀, z₀) и пусть:

x=х₀+Scosa

y=y₀+Scosb

z=z₀+Scosg

Согласно определению и правилу дифференцирования сложных функций имеем:

так как , , 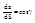то имеем:

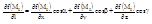(1)

Таким образом доказана теорема: Пусть функция f дифференцируема в точке (x₀, y₀, z₀), тогда в этой точке функция f имеет производную в этой точке по любому направлению и эта производная находится по формуле (1).

Опр.2: Вектор с координатами 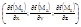называется градиентом функции f(x,y,z) в точке М₀ и обозначается grad f или символически

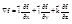
Пусть теперь вектор единичной длины, а это значит, что он имеет координаты cosa, cosb, cosg

Тогда:

(скалярное произведение)

где j – угол между векторами и gradf.

Отсюда следующие утверждения:

1. Производная функции f(x,y,z) в точке М₀ по направлению определяемом градиентом этой функции имеет максимальное значение по сравнению с производной в этой точке по любому другому направлению.

2. Значение производной функций f(x,y,z) по направлению определяемому градиентом этой функции в данной точке равно модулю градиента, т.е. равно длине вектора градиента в данной точке.

Действительно, максимальное значение производной получается при cosj=1 Þ j=0, т.е. при совпадении направления вектора с направлением вектора градиента функции.

Не нашли, что искали? Воспользуйтесь поиском: