Теорема неявно ф-ции.

Неявные функции определены одним уравнением. Выясним условие при котором одно уравнение с несколькими переменными определяет однозначную ф-цию, т.е определяет одну из переменных как ф-цию остальных.

Рассмотрим уравнение:

F(x,y)=0

Опр. Если ф-ция 2-ух переменных F(x,y)задана на некотором подмножестве А плоскости 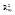и существует, такая ф-ция переменной y=f(x), определенная на множестве B Ì 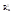содержащиеся в проекции множества А на ось ОХ, что для всех x из множества B[x,f(x)]ÎA и справедливо тождество:

F(x,f(х))=0, то ф-ция f(x) наз-ся неявной ф-цией определяемо уравнением: F(x,y)=0.

Условие существование однозначной и непрерывной неявной ф-ции.

Теорема 1: Пусть ф-ция F(x,y) непрерывна на некоторой прямоугольной окрестности т.(x₀,y₀) т.е.

U(x₀,y₀)=

При каждом фиксировании x из (x₀-h, x₀+h) строго монотонно по y на интервале (y₀-x, y₀+x), тогда если F(x₀,y₀)=0 то существуют окрестности:

U(x₀)={x| x₀-d<x< x₀+d};

U(y₀)={y| y₀-e<x< y₀+e};

То существуют окрестности т., такие что, для каждого x Î U(x₀) имеется и пи том единственное решение y Î U(y₀), ур-е:

F(x,y)=0

Это решение является ф-цией от x, и обозначается y=f(x) непрерывна в т. х₀ и f(x₀)=y₀

Т.о. эта теорема в частности утверждает что при сделанных предложениях неявная ф-ция y=f(x) определяемая уравнением F(x,y)=0 существует и обладает тем св-вом, что при условии, что x Î U(x₀), y Î U(y₀) равенства F(x,y)=0 и y=f(x)— равносильны.

Теорема 2: Пусть ф-ция F(x,y) непрерывна в некоторой окрестности т.(x₀,y₀) и имеет в этой окрестности частную производную Fпо Fy=(x,y) непрерывную в т.(x₀,y₀). Тогда если F(x₀,y₀)=0 и F(x₀,y₀)¹0, то найдутся такие окрестности U(x₀), U(y₀) соответственно т.x₀ и y₀, что для каждого x Î U(x₀) существует и при этом единственное решение y=f(x) Î U(y₀) уравнения F(x,y)=0, это решение непрерывно всюду в U(x₀) и y₀=f(x₀). Если дополнительно предположить что ф-ция F(x,y) имеет в некоторой окрестности т.(x₀,y₀) частную производную по х: (F_х(x₀,y₀) непрерывную в т.(x₀,y₀) то ф-ция f(x), также имеет производную в т.x₀ и для нее справедлива формула:

Аналогичным образом вводится понятие неявной функции, определяемо уравнением: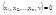

формулируется и док-во, также как т.1 и 2, под т. х₀ принимаем т. n – го пространства.

i=1, 2…n.

Пример:

F(x,y)=x²+y²-3axy=0

F(x,y,z)=e^z-xyz=0

;

;

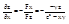Не нашли, что искали? Воспользуйтесь поиском: