Частные производные. Дифференцируемость ФМП.

Рассмотрим случай трёх переменных.

Опр.1: Пусть в некоторой окрестности точки (x₀,y₀,z₀) задана функция: U = U(x,y,z)

Фиксируя переменные y и z (y = y₀, z = z₀) получим функцию одной переменной x U(x,y₀,z₀). Обычно производная этой функции в точке х равная х₀называется частной производной функции U(x,y,z) в точке x₀,y₀,z₀по x, и обозначается:

Таким образом

Из определения обычной производной можно записать x = x₀+дельта x

Аналогично вводятся частные производные по y и z.

Частное приращение по х это:

и обозначается дельта xU. И тогда:

По аналогии с функциями одной переменной линейные функции:

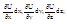
относительно dx, dy, dz соответственно называемых дифференциалами независимых переменных называются частными дифференциалами функции U(x,y,z), соответственно по переменным x, y, z и обозначаются:

Аналогичные определения имеют место для любого числа переменных.

Пример: ln(x²+ y²);

Дифференцируемость функции в точке.

Случай n = 2.

Пусть функция z = f(x,y), определена в некоторой окрестности U = U(M₀,δ),точка M₀с координатами (х₀,y₀) и пусть точка M(x,y) є U(M₀,δ). x = x - х₀; y = y - y₀; Тогда расстояние:

Пусть z = f(х₀+ x,y₀+ y) - f(x₀,y₀) - полное приращение функции.

Опр.1: Пусть функция z = f(x,y) называется дифференцируемой в точке х₀,y₀если существует 2 таких числа А и В, что: z = А х + В y + α( x, y), (1)

где: при : α(∆x, ∆y) = ε(∆x, ∆y)∙ρ, (2)

Это:

Из (1) следует, что α(0,0) = 0;

В таком случае α (∆x, ∆y) = 0(ρ), ρ→0

0 - БМВ с большим порядком малости.

В случае дифференцируемости функции z = f(x,y), в т. (х₀,y₀) линейная функция: А ∆х + В ∆y, относительно ∆х, ∆y называется полным дифференциалом функции z = f(x,y) в т. (х₀,y₀) и обозначается:

dz = А ∆х + В ∆y, или dz = Аdх + Вdy

Лемма: условие (2) эквивалентно условию:

где: и

Теорема 1: Если функция z = f(x,y) дифференцируема в т. (х₀,y₀), то она непрерывна в этой точке.

Доказательство: Т.к. функция z = f(x,y) дифференцируема, то ∆z = А ∆х + В ∆y + α (∆x, ∆y)

где: α (∆x, ∆y) = 0(ρ)

где: 0 - БМВ более высокого порядка малости, ρ →0

Т.к | ∆х|< ρ; | ∆y|< ρ; и если ρ →0 то ∆y→0 и ∆x→0

А тогда при ρ →0 из (1) следует, что ∆z→0 Что означает что функция z = f(x,y) непрерывна в т.(х₀,y₀).

Теорема 2: Если функция z = f(x,y) дифференцируема в т. (х₀,y₀) и dz = А ∆х + В ∆y, её дифференциалом в этой точке, то в точке (х₀,y₀) у функции f(x,y) существуют все частные производные: и

то

Доказательство: Согласно опр. дифференцируемости и Лемме

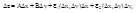
где: и

Полагая, что ∆y = 0, получим, что

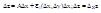
В этом случае | ∆х|= ρ;

Если, ρ →0, то ∆x→0 и ε1→0

Тогда: это есть

Аналогично полагая ∆x = 0 и переходя к пределу при ∆y→0 получим:

Следствие: если z = f(x,y) дифференцируема в точке (х₀,y₀), то она имеет единственный дифференциал.

Доказательство: единственности дифференциала следует из ф.

т.к. частные производные в точке определяются однозначно.

Полный дифференциал есть сумма частных дифференциалов:

Достаточным условием в терминах доказательств частных производных на диф-мости функции.

Теорема: Пусть z = f(x,y) в некоторой окрестности точки (х₀,y₀) имеют частные производные

........ непрерывна в точке (х₀,y₀). Тогда z = f(x,y) дифференцируема в этой точке.

Следствие: если z=f(x,y) в некоторой т.(x₀,y₀) имеет частные производные, при чем непрерывны в т. (x₀,y₀), то ф-ция z=f(x,y), также непрерывна в это т.

Не нашли, что искали? Воспользуйтесь поиском: