Функции многих переменных.

Множество на плоскости и в пространстве.(топология в Rⁿ)

Опр.1: Точка х – n-мерного пространства называется упорядоченная совокупность n действительных чисел.

Число х_i, i=1,2,…,n называется i-ой координатой точки х. Расстояние между точками: называется величена определяемая по формуле:

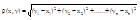(1)

Совокупность точек n-мерного пространства, для которых определено расстояние, согласно формуле (1) называется n-мерным арифметическим евклидовым пространством и обозначается: Rⁿ

Здесь длина вектора, точки х и y. Обозначение может быть:

Расстояние в обладает следующими свойствами:

1.

2. (симметрия)

3. пер-во треугольника;

Опр.2: Пусть и совокупность всех точек y пространства Rⁿ, таких что, 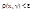называется n-мерным шаром с центром в точке х и радиусом , или - окрестностью (сферической окружностью), и обозначается:

Таким образом 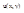- множество точек у где для которых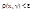

В координатной форме это определение выглядит так:

при: и .

Рассмотрим: при n=1 Rⁿ совпадает с прямой, - это интервал длины с центром в точке х.

Рис. - окрестность точки х

Если n=2, Rⁿ совпадает с плоскостью.

это: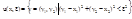

это круг радиуса с центром в точке х с координатами

При n=3:

это:

это шар радиусом , с центром в точке х с координатами

Опр.3: Пусть 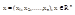и ,

где: i=1,2,…,n множество.

называется n-мерным параллелепипедом; а точка х – его центром.

Опр.4: Есл , то - называется n-мерным кубом с центром в точке х, и обозначается

Пусть n=1, то , является интервалом с центром в точке х, длины , и

n=2, то это прямоугольник со сторонами || осям координат и длинами соответственно равными и .

При n=3 – параллелепипед - Ошибка! Ошибка связи. - куб;

Опр.5: Всякий n-мерный параллелепипед называется прямоугольной окружностью точки х, -кубическая окрестность точки х.

Лемма: Каковы бы не была окрестность у точки , существует ее прямоугольная окрестность.

, такая что (целиком содержится) и наоборот, какова бы не была прямоугольная окрестность точки , существует ее окрестность такая, что

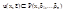
а во всякий прямоугольник можно поместить круг с ……. в центре прямоугольника n=3 параллелепипед, шар. Не трудно записать и доказать эти утверждения и в аналитической форме, использовав координатную запись, а затем обобщить на случай n-мерного пространства.

Опр.6: Множество называется ограниченным если n-мерный шар , такое что

Опр.7: Пусть каждому натуральному числу m поставлена в соответствии некоторая точка X^(m)ÎRⁿ (не обязательно родные точки для родных m). Тогда множество состоящее из точек пространства Rⁿ различными номерами называются последовательностью этого пространства и обозначается (X^m_k) k=1,2…, или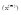

Последовательность Y^(k) называется последовательностью последовательности (X^(m)) и обозначается: (X^m_k) k=1,2…,

Если для любого k существует такое m_k что Y^(k)=X^m_k, причём, если k’< k’’,или m_k’<m _k’’.

Опр.8: Точка XÎ Rⁿ называется пределом последовательности X^m и пишется:

если

как и в случае числовой последовательности можно сказать, что , если всякая окрестность точки C содержит почти все точки данной последовательности, т.е. за исключением может быть конечного числа ux.

Не нашли, что искали? Воспользуйтесь поиском: