Геометрический смысл. (условие диф-ти ф-ции 2-ух переменных).

Пусть z=f(x,y) определена на некотором открытом множестве G Ì R². Пусть.(x₀,y₀) ÎG, если ф-ция диф-ма в т.(x₀,y₀),. То ее приращение представлено в виде:

Dz=f(x,y)-f(x₀,y₀)=ADx+BDy+V(r),r®0

или иначе: z-z₀= ADx+BDy+0(r),r®0,

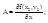
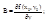
z-z₀= A(x-x₀)+B(y-y₀)+0(r), r®0

где z-z₀= A(x-x₀)+B(y-y₀) – ур-ние пл-ти, проходящей через т. (x₀,y₀,z₀);

нормальный вектор: ;

А,В – однозначно определены, следовательно плоскость определена однозначно.

Опр. Касательной пл-тью к графику функции z=f(x,y) в данной т. (x₀,y₀,z₀) называется такая пл-ть, что разность ее аппликаты и значения f(x,y) явл-ся ее величиной бесконечно малой при сравнении с r, r®0.

Т.о. ур-ние касательной имеет вид:

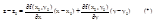
Из условия диф-ти ф-ции z=f(x,y) т.(x₀,y₀) вытекает из существования касательной к пл-тик графику этой ф-ции в т.(x₀,y₀,z₀);

Dx=x-x₀; Dy=y-y₀;

- полный диф-л ф-ции z=f(x,y) в т.(x₀,y₀).

Поэтому выражение (*) можно переписать в виде: z-z₀=dz

Т.о. геом. полный диф-ал в т.(x₀,y₀) равен приращению аппликаты плоскости касательной к графику ф-ции.

Ур-ние нормали:

.

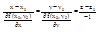Не нашли, что искали? Воспользуйтесь поиском: